|
[A:95v] 54a Si coni sectionem, vel circuli periferiam duae lineae tangentes coincidant: per tactus autem aequidistantes ducantur tangentibus et a tactibus per idem punctum periferiae lineae secent ipsas aequidistantes; 1 contentum rectangulum sub abscissis ad quadratum, quod fit ex coniungente tactus rationem habet compositam ex ea, quam habet portio interior connectentis concursum tangentium1 cum puncto medio iungentis tactus, ad portionem exteriorem potentia: et ex ea, quam habet contentum sub tangentibus ad quadratum, quod ex dimidia iungentis tactus.
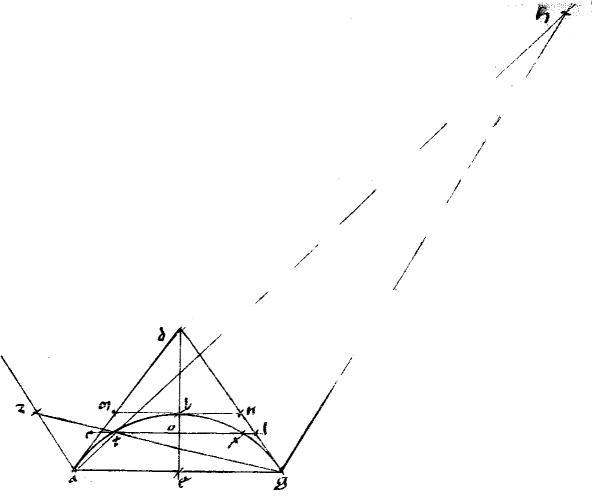
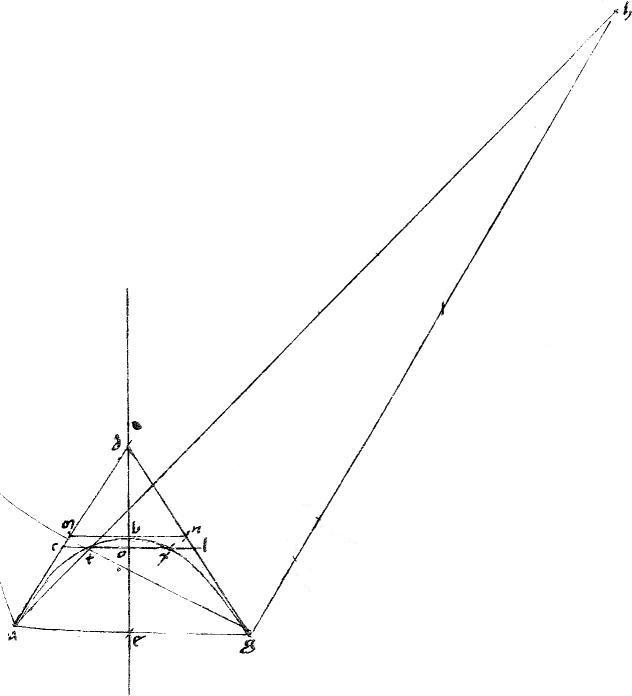
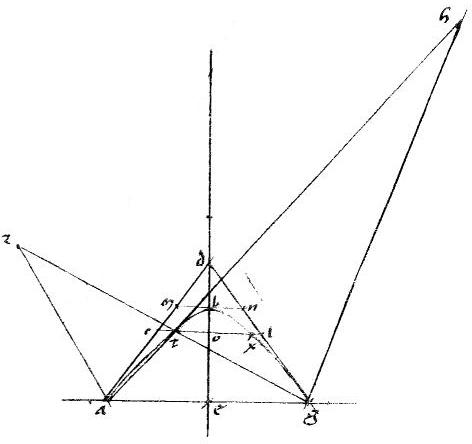2 Sit coni sectio, vel circulus abg. // Tangentes adg. // Et coniungatur ag et per medium secetur apud e. // Et coniungatur dbe2. // Ipsique gd aequidistans ducatur az. // Ipsi autem ad aequidistans gh. // Et per relictum in periferia punctum t agantur ath gtz. |
|
// Dico iam quod ratio  az gh   ag componitur ex rationibus |
|
. |
|
|
// 3 Sint enim3 ctoxl mbn penes ipsam ag. // Et quoniam ae aequalis eg erit propter similitudinem  mb aequalis bn. // Itemque co aequalis [S:126] ol. // Et quia tx ordinata, to aequalis4 ox. // ct aequalis xl. // Eritque per 16am huius tertii, sicut am mbn sic ac xct hoc est ltc5. 4 // Propter similiter autem sectas, ut ng ma ma sic lg ca ca. // Igitur ex aequo, ut ng ma 6 mbn sic lg ca ltc. |
|
|
// Verum per 24am sexti Euclidis ratio lg ca ltc componitur ex rationibus |
|
. |
|
|
|
|
|
5 Hoc est, propter similitudinem triangulorum, ex rationibus |
|
. |
|
|
Ex quibus componitur ratio hg za ga. // Ut igitur hg za ga sic ng ma 7 mbn. |
|
|
// Sed, posito medio mdn [A:96r] ratio ng ma 8 mbn componitur ex rationibus |
9 |
. |
|
|
6 // Ergo et ratio hg za ga componitur ex iisdem. // Sed propter similitudinem et proportionem figurarum, ut ng am mdn sic eb bd utque mdn mbn sic adg aeg10. |
|
|
// Itaque et ratio hg za ag componetur11 ex rationibus |
|
. |
|
|
7 // Et hoc est, quod proponebatur demonstrandum.
|
