|
1 [A:95r] 53a Si in hyperbole, vel ellipsi, vel circulo, vel contrapositis a summitate diametri ducantur ordinate applicatae: et ab eisdem terminis diametri lineae super unum punctum periferiae se invicem secantes vicissim ap[S:125]plicatis inciderint: contentum sub abscissis portionibus applicatarum aequale erit speciei, quae ad eandem diametrum.
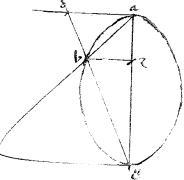
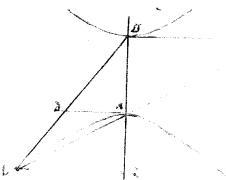2 Sit una dictarum sectionum abg. //Cuius diameter ag. // Et ordinate applicentur ad ge. // Et producantur abe dbg. // Dico iam quod   ad eg aequale est speciei, quae ad ag. // Ducatur enim ordinate applicata bz. // Eritque, per 21am primi Conicorum sicut  zb azg sic recta transversam ag et sicut species, quae ad ag ag. 3 // Quandoquidem dicta species est1 quadrato axis minoris vel diametri coniugatae2: atque recta 3 axis minor, sive diameter coniugata4 5 ag sint in proportionem continua, per corollarium 13ae vel 15ae primi Conicorum. |
|
|
// Verum per 24am sexti Euclidis ratio zb azg componitur ex rationibus |
|
. |
|
|
|
|
|
4 // Igitur et ratio speciei ag componitur ex iisdem |
|
. |
|
|
// Sed propter similitudinem triangulorum sicut bz za sic eg ga. // Itemque sicut bz zg sic da ag. |
|
|
5 // Ergo ratio speciei ag componetur ex rationibus |
|
. |
|
|
Ex quibus per 24am 6i Euclidis componitur ratio ad eg ag. // Quare sicut ad eg ag sic species ag. // Itaque6 per 9am quinti ad eg aequale7 speciei dictae, quae ad ag8. 6 // Quod est demonstrandum .
|
