F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 43
<- App. -> <- = ->

1 43a Si hyperbolen linea tangat, abscindet a non tangentibus ad centrum sectionis lineas aequale continentes contento sub abscissis lineis a tangente sectionem apud extremum axis.

[A:90v] [S:120]

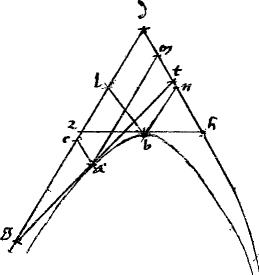figura 1
Sit hyperbole ab. // Non tangentes autem gde. // Axis bd. // Tangens apud b zbh1. // Tangens, ut contingit gat apud a quodvis punctum. 2 // Dico iam quod ad rettangolo gdt aequale est quadrato2 zdh. Ducantur enim ipsi de aequidistantes ipsae ac bl ipsique dg aequidistantes ipsae am bn. // Et, quoniam, per 3am secundi Conicorum ga aequalis at ideo, per 2am sexti Euclidis gc aequalis cd. // Ergo gd dupla ipsius dc. 3 // Et similiter td dupla ipsius dm. // Itaque ad rettangolo gdt quadruplum est rettangololi cdm. // Non aliter demonstrabimus quod et ad rettangolo zdh quadruplum est rettangolo ldn. // Verum, per 12am secundi Conicorum, aequale est ad rettangolo cdm3 rettangololo ldn. // Igitur et quadruplum quadruplo, hoc est ad rettangolo gdt rettangolo zdh aequale est: sicut proponitur demonstrandum.

Corollarium

4 Unde manifestum est, quod duabus lineis ut cumque tangentibus hyperbolen; abscissae lineae de non tangentibus ab una tangentium continent tetragonum ei, quod ex iisdem abscissae lineae a reliqua tangente continent4 tetragono.

Inizio della pagina
 ->