|
42a Si hyperbole, vel ellipsi, vel circulo, vel contrapositis ab extremis diametri ducantur ordinate applicatae: et alia quaedam ut contingit tangens sectionem agatur; tangens abscindet ab applicatis lineas, sub quibus contentum tetragonum est quadrans speciei diametro adiacentis.
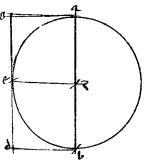
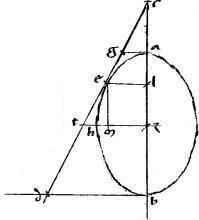
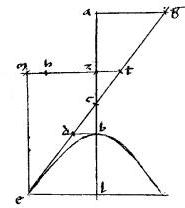 1 Sit enim quaevis dictarum sectionum be. // Cuius diameter ab. // Centrum z. // Ad extrema diametri applicatae ag bd. // Tangens ged. // Punctum tactus e. // Dico iam quod
1 Sit enim quaevis dictarum sectionum be. // Cuius diameter ab. // Centrum z. // Ad extrema diametri applicatae ag bd. // Tangens ged. // Punctum tactus e. // Dico iam quod   ag bd quadrans est speciei ad ab. // Nam, si zh coniugata ipsi ab diametro in ellipsi et circulo per e punctum it: tunc, per additam 32ae primi, aequidistabit dg ipsi ab et perinde ag zh bd sunt aequales quare tunc ag bd quadrans est speciei ad ab. // Nam, si zh coniugata ipsi ab diametro in ellipsi et circulo per e punctum it: tunc, per additam 32ae primi, aequidistabit dg ipsi ab et perinde ag zh bd sunt aequales quare tunc  1 ag bd est ipsum 1 ag bd est ipsum  zh2 quod est quadrans speciei ad ab quandoquidem per 13am vel 15am primi Conicorum, tota diameter, quae [A:90r] dupla est ipsius zh possit3 totam speciem diametri ab. 2 // Quare tunc manifesta est propositio. // Sed iam zh non veniat per e punctum tunc autem per 24am et 25am primi Conicorum, deg tangens coincidet ba diametro. // Coincidat ad c. // Et zh concurrat tangenti apud t. // Sintque el ipsi zh. // Et em ipsi ab aequidistantes. // Quibus peractis, quoniam, per 37am primi Conicorum, zh2 quod est quadrans speciei ad ab quandoquidem per 13am vel 15am primi Conicorum, tota diameter, quae [A:90r] dupla est ipsius zh possit3 totam speciem diametri ab. 2 // Quare tunc manifesta est propositio. // Sed iam zh non veniat per e punctum tunc autem per 24am et 25am primi Conicorum, deg tangens coincidet ba diametro. // Coincidat ad c. // Et zh concurrat tangenti apud t. // Sintque el ipsi zh. // Et em ipsi ab aequidistantes. // Quibus peractis, quoniam, per 37am primi Conicorum,   czl aequale est czl aequale est  az. Ideo per 15am sexti Euclidis erit, ut cz az. Ideo per 15am sexti Euclidis erit, ut cz  za sic za za sic za  zl. 3 // Et conversim, ut az zl. 3 // Et conversim, ut az  zc sic lz zc sic lz  za. // Et coniunctim, ut ac za. // Et coniunctim, ut ac  cz sic la cz sic la  az sive zb. // Et permutatim4, ut ca az sive zb. // Et permutatim4, ut ca  al sic cz al sic cz  zb. // Et rursus conversim, ut la zb. // Et rursus conversim, ut la  ac sic bz ac sic bz  zc. // Et rursus coniunctim5 ut lc zc. // Et rursus coniunctim5 ut lc  ca sic bc ca sic bc  cz. // Propter similitudinem autem triangulorum est ut lc cz. // Propter similitudinem autem triangulorum est ut lc  ca sic le ca sic le  ag. // Utque bc ag. // Utque bc  cz sic bd cz sic bd  zt. 4 Igitur ut bd zt. 4 Igitur ut bd  zt sic el zt sic el  ga. // Quare, per 15am sexti Euclidis ga. // Quare, per 15am sexti Euclidis   bd ga aequale est bd ga aequale est  zt el hoc est zt el hoc est  tzm. // Sed, per 38am primi Conicorum tzm. // Sed, per 38am primi Conicorum   tzm aequale est tzm aequale est  zh hoc est quadrans6 speciei ad ab. // Ergo et zh hoc est quadrans6 speciei ad ab. // Ergo et   bd ga quadrans est eiusdem speciei. // Quod fuit demonstrandum. bd ga quadrans est eiusdem speciei. // Quod fuit demonstrandum.
|


