F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 30
<- App. -> <- = ->

[A:82r]

// Lemma

figura 1
Esto linea mz secta in tria mn nd dz sitque rettangolo mzd cum quadrato dn simul aequale1 quadrato zn. 1 // Dico iam quod md per medium secatur apud n.

// Secus enim sit k punctum mediae2 sectionis.
// Eruntque per 6am secundi Euclidis
rettangolo mzd angolare chiusa
quadrato dk
similiter
3 		aequalia quadrato zk.
// Quam ob rem, quanto quadratotum zn maius est quadratoto zk tanto oportet quadratotum dn maius esse quadratoto dk. 2 // Sed per 4am 2i Euclidis quadrato zn maius est quadratoto zk in rettangolo rettangolo 4 zkn et quadrato nk.Et quadrato dr5 maius est quadratoto dk in rettangolo rettangolo6 dkn et quadrato nk. // Aequalia ergo sunt rettangolo rettangolo7 zkn cum quadrato nk ipsis rettangolo rettangolo8 dkn et quadrato nk. // Commune auferatur quadrato nk erunt relicta aequalia: et eorum dimidia scilicet rettangolo zkn rettangolo9 dkn aequalia, pars et totum quod est impossibile. // Igitur md non alibi, quam apud n per medium secatur. 3 // Quod est propositum.

30a Si hyperbolen duae lineae tangentes coincidant, et tactus linea10 coniungat11: quae a concursu tangentium penes unam non tangentium ad tactus coniungentem, linea ducitur, per aequalia secatur a periferia sectionis.

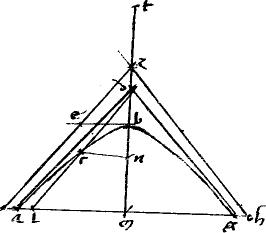figura 2
4 Sit hyperbole abg. // Non tangentes ezh. // Tangentes adg. // Coniungens tactus ag. // Cui apud l incidat dcl aequidistans ipsi ze, quae, per 13am 2i in uno puncto coincidet sectioni, ut apud c. // Dico iam quod dl per medium secatur apud c. 5 // Coniungatur enim dz et producatur: sitque bz aequalis zt. // Et ordinate agantur be cn. // Eritque, propter similitudinem et proportionem triangulorum quadrato dn ad quadrato nc sicut quadrato zb ad quadrato be et ideo, sicut tb ad rectam quandoquidem12 dupla sunt dimidiis proportionalia. // Et per 21am primi Conicorum sicut rettangolo tnb ad quadrato nc. // 6 Quare per 9am quinti Euclidis rettangolo tnb aequale est quadrato dn. // Est autem, per 37am primi Conicorum rettangolo mzd aequale quadrato zb. // Quandoquidem ad tangens et am applicata13 . // Ergo rettangolo tnb cum quadrato zb simul aequale est14 rettangolo mzd et quadrato dn simul sumptis. // Sed per 6am 2i Euclidis rettangolo tnb cum quadrato zb aequale est quadrato zn. // Igitur et quadrato zn [S:111] aequale fit ipsis rettangolo mzd quadrato15 dn simul. 7 // Quam ob rem per lemma praemissum [A:82v] ipsa md per medium secatur apud n. // Cumque cn lm sint aequidistantes; iam per 2am 6i Euclidis et ipsa dl per aequalia similiter secatur apud c. // Id scilicet, quod proponebatur demonstrandum.

Inizio della pagina
 ->