F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 31
<- App. -> <- = ->

// Lemma

figura 1
Esto linea gd secta in tria gx xe ed.
// Sitque quadrato gx aequale
angolare aperta quadrato xe
rettangolo ged
simul acceptis.
1 // Aio quod gd per aequalia secatur apud x. // Secus enim sit k punctum bifariae sectionis.
// Eritque, per 5am secundi Euclidis quadrato gk aequale
angolare aperta quadrato ke
rettangolo ged
.
Quare maius quadrato gx quadratoto gk pars toto. // Quod est impossibile. // Itaque gd non alibi quam1 apud x secatur per aequalia. // Quod ostendendum proponitur.

2 31a Si contrapositas duae lineae tangentes coincidant: et per tactus linea producatur per coincidentiam vero ducatur linea penes non tangentem secans sectionem et tactus coniungentem; quae est inter coincidentiam et tactus coniungentem, per aequalia secabitur a periferia sectionis.

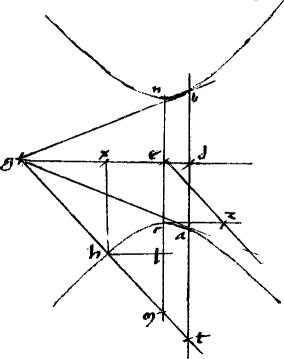figura 2
3 Sint contrapositae a b. // Tangentes agb. // Coniungens tactus bat. // Non tangens ez. // Centrum e. // Aequidistans ipsi ez ipsa ght secansque periferiam apud h per 13am 2i occurrens autem ipsi ba apud t. // Dico iam quod gt per medium secatur apud h. // 4 Coniungatur enim ge occurratque ipsi ab apud d. // Et per puncta e h penes ipsam ab ducantur eclmn hx. // Et penes gd ipsae cz hl. // Eritque, propter similitudinem triangulorum cze lhm sicut quadrato ec ad quadrato cz sic quadrato ml ad quadrato lh. // Et, quoniam ec 1/2 ipsius nc transverso2 et cz sit 1/2 2ae diametri (cum per 3am 2i Conicorum, possit quadrantem speciei ad nc )3 atque nc ad4 secunda diameter ad rectumque latus sint continue5 proportionales. 5 Et perinde sicut quadrato nc ad quadrato 2ae diametri, sic nc ad rectum: et ideo, sicut quadrato ec ad quadrato cz. // Propterea iam, per 21am primi Conicorum, [A:83r] erit, ut quadrato ec ad quadrato cz sic rettangolo nlc ad quadrato lh. // Fuit autem et sic quadrato ml ad quadrato lh. // Igitur, per 9am quinti Euclidis quadrato6 ml aequale est rettangolo nlc.
6 // Quam ob rem
rettangolo nlc angolare chiusa
quadrato ce
simul aequalia sunt
angolare aperta quadrato ml
quadrato ce
simul sumptis.
Hoc est per 6am secundi Euclidis quadrato el sive xh aequale est
angolare aperta quadrato ml
quadrato ce
una coniunctis.
// Propter similitudinem autem et proportionem laterum triangulorum sicut quadrato hx ad quadrato quadrato ml ce sic quadrato xg ad quadrato quadrato hl cz. 7 // Aequale ergo, sicut primum secundo sic tertium quarto hoc est quadrato xg ad quadrato quadrato hl cz simul sumptis aequale erit. // Aequale autem quadrato lh quadratoto xe. // Aequale item quadrato cz quadratoto dimidii secundae diametri. Et ideo aequale rettangolo ged per 38am primi Conicorum. // Igitur et quadrato xg aequale erit quadrato xe et rettangolo ged simul sumptis. // Quare, per lemma prae[S:112]missum gd per aequalia secatur apud x. // Verum xh aequidistat ipsi dt. // Ergo, per 2am sexti Euclidis et ipsa gt per [S:113] medium secatur apud h. 8 // Quod quidem proponebatur demonstrandum.

Inizio della pagina
 ->