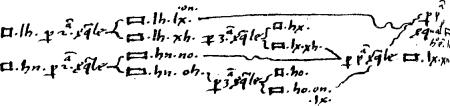F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 29
<- App. -> <- = ->

[A:81v]

// Lemma

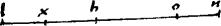figura 1
1 Esto linea ln secta in quatuor divisiones lx xh ho on ita ut extremae portiones lx on sint aequales.

// Dico iam quod
quadrato lh angolare chiusa
quadrato hn
similiter
1 		aequalia sunt his
graffa aperta quadrato xh
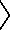angolare chiusa simul
quadrato ho
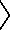rettangolo lxn angolare chiusa quae eadem sunt
rettangolo lon
2 		.
2 // Quod ex 2a 3a pa secundi Elementorum sic ostenditur. quadrato lh per 2am

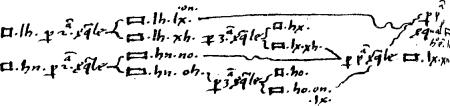figura 2
3
// Igitur
quadrato lh angolare chiusa
quadrato hn
4 		simul aequalia fient his quattuor
videlicet
graffa aperta quadrato hx
quadrato ho
rettangolo lxn
rettangolo lon
5 		. Quod est propositum.

3 29a Iisdem subiectis, si aequidistans rectae secet non tangentes: quadrata, portionum6 aequidistantis rectae ab incidentia ductarum ad non tan[S:110]gentes receptarum accipientia dimidium quadrati quod fit ex recta, ad quadrata portionum aequidistantis transversae ab incidentia ad periferias receptarum, rationem habent eam, quam quadratum rectae ad quadratum transversae.

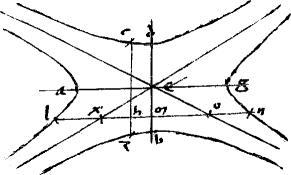figura 3
4 Sint enim eadem, quae prius. // Et ln secet non tangentes apud x o. // Demonstrandum est, quod quadrato quadrato xh ho cum 1/2 quadrato ti ag hoc est cum quadrato quadrato7 ea vel rettangolo rettangolo8 lxn ad quadrato quadrato zh hc rationem habent, quam quadrato ag ad quadrato bd. // Cum enim per 8am secundi Conicorum lx on sint aequales iam per praecedens lemma quadrato quadrato lh hn aequalia erunt quadrato quadrato xh ho et rettangolo rettangolo9 lxn hoc est quadrato quadrato10 ea per 11am 2i Conicorum. 5 // Sed per praemissam quadrato quadrato lh hn ad quadrato quadrato zh hc sunt sicut quadrato ag ad quadrato bd. // Igitur et quadrato quadrato xh ho cum quadrato quadrato11 ea ad quadrato quadrato zh hc sicut12 quadrato ag ad quadrato bd. // Sicut erat demonstrandum.

Inizio della pagina
 ->