F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 27
<- App. -> <- = ->

27a Si ellipseos1 vel circuli periferiae coniugatae diametri ducantur, et dicatur2 earum altera recta, altera transversa: et penes ipsas ducantur duae lineae coincidentes invicem et periferiae; quadrata, quae fiunt ex receptis portionibus a linea penes transversam ducta, accipientia species, quae fiunt ex continuatis portionibus ad lineam penes rectam ductam, similes et similiter descriptas subiectae speciei ad rectam diametrum, aequalia erunt quadrato, quod fit ex transversa diametro.

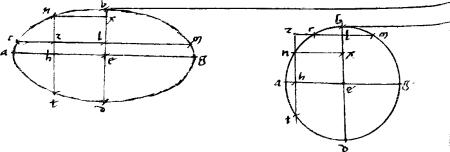figura 1
1 Sit enim ellipsis, vel circulus abgd. // Cuius centrum e. // Coniugatae diametri, recta quidem aeg. // Transversa autem bed. // Et penes ipsas ag bd ducantur nzht czlm.
// Dico iam quod
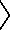quadrato nz cum specie ex cz angolare chiusa
quadrato zt cum specie ex zm
simili
 speciei, quae ad ag aequalia sunt ipsi quadratoto bd.
2 // Ducantur enim penes ae ordinate iam nx. // Itemque ipsa bp ad quam possunt ordinate ductae. // Eritque, per 15am primi Conicorum, sicut bp ad bd sic quadrato ag ad quadrato bd. // Sed per corollarium 13ae primi Conicorum quadrato bd aequale est speciei, quae adiacet ipsi ag. // Igitur sicut bp ad bd sic quadrato ag ad speciem, quae ad ag. 3 // Et propter similitudinem figurarum, sic quadrato nx ad speciem nx similem speciei ag3 [A:80v] // Est autem per 21am primi Conicorum ut bp ad bd sic quadrato nx ad rettangolo bxd. // Ergo per 9am quinti Euclidis species nx hoc est zl similis speciei ag4 aequalis est rettangolo bxd. // Et similiter demonstrabimus quod species cl similis speciei ag aequalis est rettangolo bld5. // 4 Et quoniam nt secatur per aequalia apud h et per inaequalia apud z ideo per 9am secundi Euclidis quadrato quadrato6 tz zn simul sumpta dupla sunt quadrato quadratotorum th hz hoc est quadrato quadrato nh hz. // Et eadem adducta quadrato quadrato mz zc simul iuncta dupla sunt quadrato quadrato cl lz. Itemque propter similitudinem et proportionem figurarum species mz zc similes speciei ag simul dupla sunt similium specierum cl lz. 5 // Aequales autem fuere species cl lz ipsis rettangolo rettangolo bxd bld. // Atque ob aequalitatem laterum quadrato quadrato nh hz aequalia ipsis quadrato quadrato7 xe el. // Igitur quadrato quadrato tz zn cum [S:109] speciebus mz zc similibus speciei ag dupla sunt rettangolo rettangolo bxd bld et quadrato quadrato xe el simul. 6 // Et quoniam bd secatur per aequalia apud e et per inaequalia apud x ideo, per 5am secundi Euclidis rettangolo bxd cum quadrato xe aequale est quadrato be. // Et per eandem rettangolo bld cum quadrato le aequale est quadrato be. // Quare rettangolo rettangolo bxd bld cum quadrato quadrato xe el aequalia sunt quadrato quadrato8 be. // Et propterea quadrato quadrato tz zn cum speciebus mz zc similibus speciei ag dupla sunt quadrato quadrato9 be. 7 // Et perinde quadrupla quadrato be. // Et ideo aequalia quadrato bd. // Quod fuit demonstrandum.

Inizio della pagina
 ->