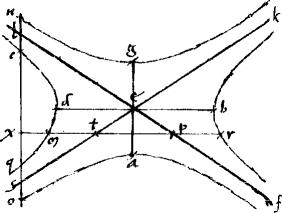
1 [A:78v] 25a Iisdem subiectis, sit concursus aequidistantium ipsis1 ag bd intra alteram sectionum db ut supponitur, apud x punctum; dico tunc, quod contentum sub portionibus aequidistantis transverso, id est, 
oxn eo rectangulo (ad quod rationem habet [S:106] contentum sub portionibus aequidistantis recto, id est rxm eam, quam id, quod fit ex recta ad id, quod ex transversa) maius erit quadrato2, quod bis fit ex dimidio transversi.
|
rxm sicut 
db 
ag. //Nam per eadem, quae prius, ut4 de ea in tertio casu sic pxt sxl5. //Sed per 11am 2i Conicorum de aequale est pmt. //Et per 10am eiusdem ae aequale est lqs6. 3 //Igitur, sicut 7 pxt lxs8 totum videlicet ad totum, sic pmt lqs9 ablatum ad ablatum. // Quam ob rem rxm qxc reliquum ad reliquum, sicut pxt lxs10 totum ad totum et perinde, sicut de ea hoc est db ag. 4 (//Nam, cum linea rx secta sit in partes quatuor, ita ut ipsae rp tm sint aequales, per 16am 2i iam per scholium 22ae huius rxm una cum pmt aequale est pxt. Itemque, cum linea ls11 secta sit quadrifariam, ita ut extrema segmenta lc12 qs sint aequalia per 8am 2i Conicorum, iam per primum lemmatum praemissae lqs13 cum qxc simul aequale fit lxs14//). 5 // Demonstrandum igitur15, quod oxn aequale est qxc una cum 16 ae. //(Cum autem linea on secta sit in quatuor partes, quarum extremae os ln17 sunt aequales, per 16am 2i18 reliquae autem sx xl19 iam per primum lemmatum praecedentis, lxs20 cum nso aequalia sunt oxn. // Sed ipsi lxs21 aequalia fuere lqs qxc22. 6 // Et ideo tria rectangula23 scilicet lqs24 qxc nso simul sumpta aequalia sunt lo oxn). //Itaque tam a oxn quam ab aggregato qxc et 25 ae communi ablato qxc. //Demonstrandum restat, quod lqs26 cum nso aequale est 27 ae. 7 // Est autem quoniam videlicet, per 11am secundi Conicorum nso hoc est los28 aequale est ae et per 10am vel 22am29 eiusdem lqs30 aequale est ae. //Quam ob rem, verum est, quod proponitur demonstrandum.