|
[A:75v] 1 22a Si contrapositas duae lineae aequidistantes tangant: ducantur autem quaedam lineae secantes invicem et sectiones, altera quidem penes tangentem, altera vero penes1 tactus coniungentem; erit, ut transversum latus speciei (quod aequidistat iungenti tactus) ad rectum; sic contenta sub se invicem secantium segmentis ab incidentia receptis ad periferias sectionum.
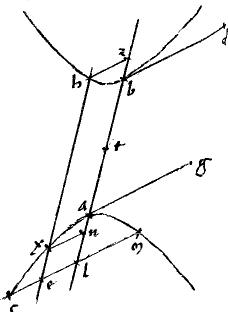 2 [S:101] Sint contrapositae a, b. // Tangentes paralleli ag, bd. // Et coniungatur ab. // Ipsa autem exh aequidistans ab. // Et ipsa cem aequidistans ag secantes se invicem apud e et sectionum periferiis incidentes apud e, h, c, m2. // Dico iam quod est, ut ab transversa diameter ad rectum speciei latus, sic
2 [S:101] Sint contrapositae a, b. // Tangentes paralleli ag, bd. // Et coniungatur ab. // Ipsa autem exh aequidistans ab. // Et ipsa cem aequidistans ag secantes se invicem apud e et sectionum periferiis incidentes apud e, h, c, m2. // Dico iam quod est, ut ab transversa diameter ad rectum speciei latus, sic  hex hex   cem. 3 // Nam quod ab coniungens tactus eat per centrum sectionum, patet per conversam additae post 43am primi Conicorum, vel 31ae secundi vel per corollarium postremum dictae additae. // Ducantur itaque per h, x puncta penes ag hz3, xn et perinde ordinatae ad ab diametrum, cui cm incidat apud l iampridem similiter applicata. 4 // Eruntque per 47am primi Conicorum cl, lm aequales. // Et ideo, per per 5am 2i Euclidis erunt cem. 3 // Nam quod ab coniungens tactus eat per centrum sectionum, patet per conversam additae post 43am primi Conicorum, vel 31ae secundi vel per corollarium postremum dictae additae. // Ducantur itaque per h, x puncta penes ag hz3, xn et perinde ordinatae ad ab diametrum, cui cm incidat apud l iampridem similiter applicata. 4 // Eruntque per 47am primi Conicorum cl, lm aequales. // Et ideo, per per 5am 2i Euclidis erunt  cem et cem et  le simul aequalia le simul aequalia  lc. // Item, posito t centro sectionum, erunt, per 16am primi Conicorum ipsae tz, tn invicem aequales, et perinde, ipsae bz, an invicem aequales. 5 // Et ideo, sicut mox in scholio demonstrabitur; lc. // Item, posito t centro sectionum, erunt, per 16am primi Conicorum ipsae tz, tn invicem aequales, et perinde, ipsae bz, an invicem aequales. 5 // Et ideo, sicut mox in scholio demonstrabitur;  bna et bna et  zln simul sunt aequalia zln simul sunt aequalia  bla. // Itaque, quoniam per 21am primi Conicorum, sicut ab transversa diameter ad rectum latus speciei, sic bla. // Itaque, quoniam per 21am primi Conicorum, sicut ab transversa diameter ad rectum latus speciei, sic  bla bla   lc totum scilicet ad totum; et sic lc totum scilicet ad totum; et sic  bna bna   nx quod est4 nx quod est4  le ablatum scilicet ad ablatum. 6 // Erit, per 19am quinti Euclidis le ablatum scilicet ad ablatum. 6 // Erit, per 19am quinti Euclidis  zln zln   cem reliquum ad reliquum, sicut cem reliquum ad reliquum, sicut  bla bla   lc totum ad totum: et iam sicut ab transversa diameter ad rectum latus. // Aequale est autem lc totum ad totum: et iam sicut ab transversa diameter ad rectum latus. // Aequale est autem  hex hex  lo zln propter aequalitatem oppositorum laterum in parallelogrammo. // Igitur et lo zln propter aequalitatem oppositorum laterum in parallelogrammo. // Igitur et  hex hex   cem sicut5 ab transversa ad rectum speciei latus. // Et hoc erat demonstrandum. cem sicut5 ab transversa ad rectum speciei latus. // Et hoc erat demonstrandum.
Scholium
[A:76r]
 7 Ponatur linea zl sic divisa in quatuor segmenta: ut ipsa zb an uno intermisso ab sint aequalia:ipsa autem segmenta ba nl quantacunque. // Demonstrandum est quod
7 Ponatur linea zl sic divisa in quatuor segmenta: ut ipsa zb an uno intermisso ab sint aequalia:ipsa autem segmenta ba nl quantacunque. // Demonstrandum est quod  bna et bna et  zln simul sunt aequalia zln simul sunt aequalia  bla hoc modo. // Nam, per primam secundi Euclidis bla hoc modo. // Nam, per primam secundi Euclidis  bna et bna et  bnl simul sumpta aequalia sunt bnl simul sumpta aequalia sunt  bn al. // Et per eamdem bn al. // Et per eamdem  bn al cum bn al cum  aln conficit aln conficit  bla. 8 // Quam ob rem tria rectangula, scilicet bla. 8 // Quam ob rem tria rectangula, scilicet  bna bna  bnl bnl  aln conflabunt aln conflabunt  lum bla. // Sed, per eamdem primam 2i Elementorum (quoniam lineae bn, al faciunt lineam zl) lum bla. // Sed, per eamdem primam 2i Elementorum (quoniam lineae bn, al faciunt lineam zl)  bnl bnl  aln simul accepta integrant aln simul accepta integrant  zln. // Ergo et zln. // Ergo et  zln cum zln cum  bna similiter aequalia erunt bna similiter aequalia erunt  bla. // Quod restabat ostendendum. bla. // Quod restabat ostendendum.
|
|
|
|
|
 bna bna |
 |
 bn al bn al |
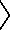 |
 bla bla |
 zln zln |
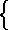 |
 bnl bnl |
|
 aln aln |
|
|
6 Additio
9 Si in una contrapositarum ad coniunctionem sectione duo puncta relicta sint: et ab ipsis binae hinc et binae inde aequidistantes lineae penes tangentes collateralium duarum sectionum ad diametros per tactuum puncta deductas permutatim applicatae producatur; facta a productis ad diametros quadrilatera aequalia invicem erunt.
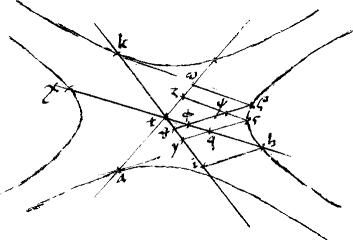 10 Sint contrapositae sectiones ad coniunctionem a, s, k, x. // In quarum una s duo puncta s
10 Sint contrapositae sectiones ad coniunctionem a, s, k, x. // In quarum una s duo puncta s 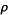 relicta sint. // Tactuum puncta a, k. // Per quae diametri atz7 kty. // Et ad ipsam atz diametrum ducantur penes tangentem apud k ipsae8 s relicta sint. // Tactuum puncta a, k. // Per quae diametri atz7 kty. // Et ad ipsam atz diametrum ducantur penes tangentem apud k ipsae8 s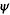 z z 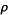 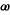 // Ad ipsam autem kty diametrum, agantur penes tangentem apud a ipsae // Ad ipsam autem kty diametrum, agantur penes tangentem apud a ipsae 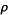 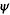 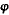  sqy9. 11 // Sic enim fiet, per 16am et 47am primi Conicorum, ut ipsae s sqy9. 11 // Sic enim fiet, per 16am et 47am primi Conicorum, ut ipsae s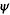 z z 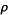 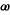 ad ipsam quidem kty diametrum et [S:102] vicissim ipsae sqy ad ipsam quidem kty diametrum et [S:102] vicissim ipsae sqy 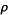 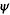 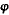  ad ipsam atz diametrum ordinate applicatae sint. // Dico itaque quod ad ipsam atz diametrum ordinate applicatae sint. // Dico itaque quod  z z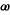 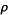 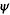 aequale est aequale est  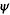  ys. 12 // Nam, ductis ad easdem diametros penes ipsas sz ys. 12 // Nam, ductis ad easdem diametros penes ipsas sz 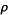 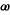 diametro quidem10 xth quae per 20am secundi Conicorum coniugata est ipsi kty diametro, quandoquidem tangenti apud k aequidistat. Itemque hi penes11 ipsam sy.// Iam ex demonstratione 15ae huius: ut in corollario ipsius concluditur, diametro quidem10 xth quae per 20am secundi Conicorum coniugata est ipsi kty diametro, quandoquidem tangenti apud k aequidistat. Itemque hi penes11 ipsam sy.// Iam ex demonstratione 15ae huius: ut in corollario ipsius concluditur,  sztq aequum erit ipsi sztq aequum erit ipsi  qhiy. Itemque, per idem corollarium qhiy. Itemque, per idem corollarium  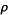 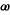 t t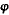 aequale erit ipsi aequale erit ipsi  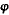 hi hi . // 13 Verum12 primis duobus, communi apposito . // 13 Verum12 primis duobus, communi apposito   q fiet q fiet  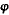 h i h i aequum aequum  zq et zq et  q q simul13. // Et ideo simul13. // Et ideo  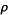 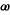 t t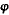 aequale iisdem aequale iisdem   zq q zq q . // Commune auferatur . // Commune auferatur  zt zt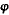 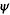 14. // Et supererit 14. // Et supererit  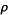 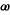 z z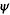 aequale iam ipsi aequale iam ipsi  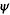  ys. // Quod scilicet proponebatur demonstrandum. 14 Et manifestum est, quod communi apposito ys. // Quod scilicet proponebatur demonstrandum. 14 Et manifestum est, quod communi apposito  t t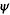   t t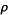 ts aequalia erunt15. ts aequalia erunt15.
|