F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 17
<- App. -> <- = ->

<17.um> Si coni sectionem, vel circuli periferia duae lineae tangentes coincidant: relicta autem sint in sectione duo contingentia puncta, et ab ipsis ducantur in sectione tangentibus paralleli se invicem secantes; erunt [S:96] ad invicem ex tangentibus quadrata, sicut contenta sub parallelorum segmentis tetragona.

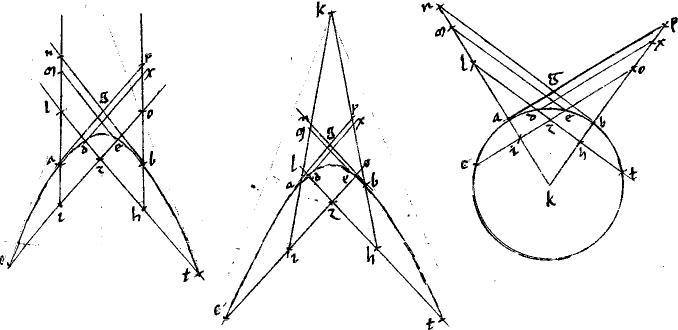figura 1
1 Sit coni sectio, vel circuli periferia ab. // Tangentes ag, gb. // Et per relicta in sectione puncta d, e tangentibus aequidistantes in sectione ducantur dzt, ezc. // Dico iam quod est sicut quadrato ga ad quadrato gb sic rettangolo cze ad rettangolo tzd. // Ducantur enim per a, b diametri almn, bxop. 2 // Quibus occurrant tangentes quidem apud n, p tangentium vero paralleli apud l, o et i, h. // Item tangentibus aequidistantes ducantur similiter usque ad diametros dx, em. // Et quoniam per 46am et 47am primi Conicorum ci1 aequalis ie2 itemque th aequalis hd. // Ideo, per 6am 2i3 Euclidis rettangolo cze cum quadrato zi simul aequalia sunt quadrato ei. 3 // Cumque sit sicut quadrato ei ad quadrato4 zi sic triangolo eim ad triangolo zil quia5 similes figurae super iisdem lineis. Et permutatim quadrato ei ad triangolo eim totum scilicet ad totum, sicut quadrato zi ad triangolo zil ablatum scilicet ad ablatum. // Erit, per 19am quinti Euclidis rettangolo cze ad trapezio zm reliquum videlicet ad reliquum6 sicut quadrato ei ad triangolo eim totum scilicet7 ad totum. 4 // Sed et sic est quadrato ga ad triangolo gam8 propter similitudinem quadratorum et triangulorum et ideo sicut rettangolo cze ad trapezio zm. // Aequale autem fuit triangolo agn triangolo gpb per primam huius: et trapezio zm aequum trapezio zx per 3am huius. // Igitur sicut rettangolo cze ad trapezio zx sic quadrato ga ad triangolo gpb. 5 // Et similiter demonstrabimus quod sicut rettangolo tzd ad trapezio zx sic quadrato gb ad triangolo gpb et conversim sicut trapezio zx ad rettangolo tzd sic triangolo gpb ad quadrato gb. // Ergo ex aequali, erit, sicut rettangolo cze ad rettangolo tzd sic quadrato ga ad quadrato gb. // Quod iam proponebatur demonstrandum.

Scholium9

Nota quod hic et in praecedenti k centrum est sectionis in ellipsi10 et circulo. 6 // Nam parabole centrum non habet.

Inizio della pagina
 ->