F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber secundus Propositio 12
<- App. -> <- = ->

11a Si altera non tangentium1 extra producta, factum angulum extrinsecum continentes lineas secet quae dam linea, coincidet2 sectioni ad unum solum punctum, et contentum sub receptis lineis, sub secante scilicet inter productam et hyperbolen, et sub eius portione inter hyperbolen et non tangentem3, aequale erit quadranti eius, quod fit4 ex diametro penes secantem ducta.

[A:43v]

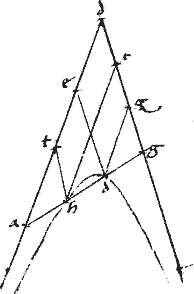
figura 1
[S:58] Sit hyperbole hb. // non tangentes5 autem ga ad. // Et producatur da usque ad e. // Et per punctum e ducatur ez secans ipsas ae ag quae iam coincidet sectioni ad unum solum punctum. Nam quae per a ducitur aequidistans ipsi ez ut abl secabit angulum gad non tangentium, et coincidet sectioni per 2am huius. Quare ez coincidet sectioni, per 26am praemissi, ad unum solum punctum. Coincidat ad ipsum h.

Dico iam quod

rettangolo ehz aequale est quadrato to ab semidiametri.

// Ducatur enim ordinate thlc coincidens non tangentibus6, sectioni, et diametro apud ipsamet t h l c puncta. Quare, per 5am huius, linea apud b tangens sectionem, quae sit gbd aequidistans est ipsi thlc.

Et quoniam per 24am Sexti Euclidis ratio quadrato 7 gbd ad quadrato ba componitur
ex rationibus
graffa aperta gbadba
dbadba
et ideo ex rationibus
graffa aperta thadhz
chadhe
.

Ratio autem rettangolo cht ad rettangolo ehz componitur ex iisdem rationibus
graffa aperta thadhz
chadhe
.

Ideo sicut

rettangolo cht ad rettangolo ehz sic quadrato 8 gbd ad quadrato ba et permutatim sicut rettangolo cht ad quadrato gbd sic rettangolo ehz ad quadrato ba.

Sed per praecedentem

rettangolo cht aequale est quadrato9 gbd quod, per 3am huius, est quadrans speciei.

Igitur et

rettangolo ehz aequale est quadrato ba. // Quod fuit demonstrandum.

Inizio della pagina
 ->