[A:28v] 46^a Si parabolen linea tangens coincidat diametro; ducta per tactum aequidistans diametro intra sectionem, ductas in sectione penes¹ tangentem per medium secabit.

Sit parabole² cuius diameter abd. // Tangens sectionem ag. // Punctum tactus g. // Ipsa tgm penes³ ipsam ad . //⁴ Per quodvis periferiae⁵ punctum l agatur lnz penes⁶ ag tangentem

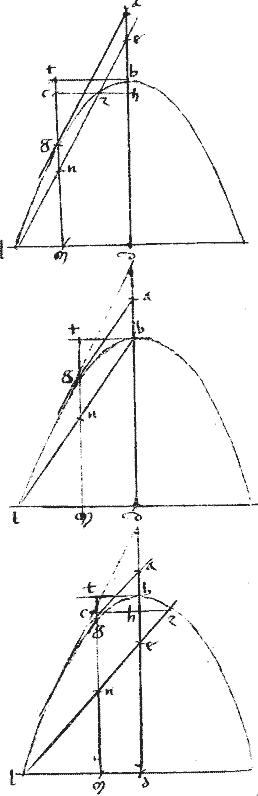
// Dico iam quod ln ⁷ aequalis est ipsi ⁸ nz.

// Ducantur enim ordinate bt et per z punctum⁹ [S:39] czh et lmd. // Atque lz producatur, donec occurrat diametro ad punctum e.

// Eritque per 42^am10 huius eld aequale ^[[lo]] bm¹¹. Itemque ezh aequale ^[[mo]] bc¹².

// Quare et residuum¹³ residuo, hoc est, [[]] hm¹⁴ aequale supererit lzhd.

// Commune auferatur, pentagonum mdhzn.

Et supererit czn aequale mln.

// Sunt autem similia ¹⁵ propter basium aequidistantiam¹⁶. Atque ob id, erunt czn mln invicem aequilatera: omnia enim duo aequalia et similia habent invicem latera lateribus singula singulis¹⁷ aequalia aequis aungulis opposita.

Igitur zn aequal ¹⁸ nl. // Quod est propositum. Continget praeterea ipsam ln coincidere diametro apud punctum b summitatem scilicet sectionis ut in 2^a lineatione.

// Et tunc quoniam per 42^am huius bdl aequum [[]] bm¹⁹. // Ablato communi trapezio²⁰ bdmn. // Supersunt btn lmn aequalia: et ideo, ut prius ln nb aequis angulis subtensae aequales. //

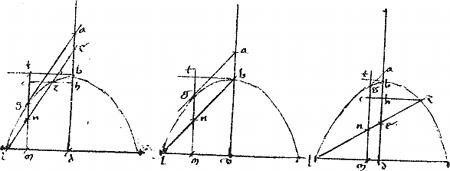
Demum accidet, ut ln diametro intra sectionem coincidat, ut pote²¹ apud e deinde producta ultra diametrum periferiae²² occurrat, ut pote²³ apud z ductisque ordinate in 3^a descriptione, ut prius.

// Erit per 42^am huius, [A:29r] edl aequale ^mo bm²⁴. // Demptoque communi trapezio edmn supererit lmn aequum ntbe²⁵. // Verum, per 42^am rursus ehz aequale est [[]] bc²⁶ et propterea, posito communi trapezio²⁷ nche. // Erit zcn aequum ntbe et perinde aequum lmn. // Quare, ut antea, cum zcn lmn sint similia, erunt invicem aequilatera: atque ideo ln nz latera aequos angulos subtendentia invicem aequalia. // Quod erat demonstrandum.

Similiter ostendemus, quod ipsa tgm non solum ipsam lz sed omnes alias lineas intra sectionem penes tangentem ductas singulas bifariam dispescit: et perinde, cum bd sit principalis diameter, ipsa tgm erit ex generatione diametros. Et similiter demonstrabimus, quod omnis linea principali diametro parallelus erit ex generatione diametros, in parabola.