[A:23r] 41^a Si in hyperbola, vel ellipsi vel circuli periferia linea applicetur ordinate ad diametrum: et ab applicata, nec non ab ea, quae ex centro describantur bina parallelogramma aequiangula: habeatque applicatum latus ad reliquum speciei¹ latus compositam rationem ex ea, quam habet, quae ex centro ad reliquum speciei² latus, et ex ea, quam habet rectum speciei sectionis latus ad transversum. Tunc species³, quae⁴ sit, ex ea, quae inter centrum et applicatam, similis ei speciei, quae⁵ ab ea, quae ex cen[S:33]tro, in hyperbola quidem maior est ea specie, quae sit ex applicata, excessu aequali ei speciei, quae sit ab ea, quae⁶ ex centro: in ellipsi vero et circuli periferia, cum ea specie, quae⁷ sit ab applicata, aequalis⁸ est ei speciei, quae⁹ sit ab ea, quae ex centro.

Sit hyperbole, ellipsis vel circulus: cuius diameter ab. // Centrum e. // Ordinate ducta gd. // Et ab ipsis ea gd aequiangulae¹⁰ species¹¹ describantur az dh¹² hac conditione,

ut ratio gd gh composita sit ex rationibus ae ez rectae transversam .

// Dico iam quod in hyperbola, species, quae¹³ sit ex ed similis¹⁴ ipsi az

aequalis est speciebus15 az dh .

//

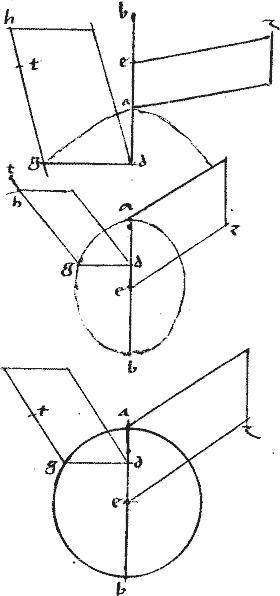
// Sit enim dg gt sicut recta transversam.

// Et quoniam dg gt sicut¹⁶ dg dgt per primam 6ⁱ Euclidis. // Et per 21^am huius ut recta transversam sic dg bda. // Ideo bda aequum est dgt.

// Et quoniam per hypothesim ratio dg gh componitur

ex rationibus ae ez rectae transversam vel dg gt .

[A:23v]

// Ratio autem dg gh componitur ex rationibus dg gt gt¹⁷ gh.

// Ideo, ablata utrinque ratione dg gt.

Superest ratio ae ez aequalis rationi gt gh.

// Sed per primam 6ⁱ Euclidis sicut gt gh sic tgd hgd et sicut ae ez sic ae aez.

// Fuitque tgd aequale bda.

// Igitur bda hgd sicut ae aez.

// Et permutatim bda ae sicut hgd aez.

// Sed hdg aez sicut species¹⁸ dh speciem¹⁹ za aequiangula²⁰ enim habent rationem compositam ex lateribus.

// Ergo bda ae sicut species²¹ dh speciem²² za.

// Et in hyperbola coniunctim bda una cum ae hoc est per 6^am 2ⁱ Euclidis ed ae erit sicut aggregatum specierum²³ dh za speciem²⁴ za.

// Ut autem ed ea sic species²⁵ ex ed similis²⁶ et similiter descripta²⁷ ipsi az ad speciem ipsam²⁸ az. // Quandoquidem sunt in dupla ratione laterum.

// Quare sicut aggregatum specierum²⁹ dh za speciem³⁰ za sic species³¹ ex ed similis³² et similiter descripta³³ ipsi az speciem ipsam³⁴ za.

// Et ideo per 9^am 5ⁱ Euclidis species³⁵ ex ed similis³⁶ ipsi az aequalis³⁷ erit aggregato speciorum³⁸ dh za in hyperbola.

// Autem in ellipsi³⁹ et circulo, conversim, disiunctim et permutatim⁴⁰. // Excessus, quo ea superat bda qui excessus, per 5^am 2ⁱ elementorum Euclidis

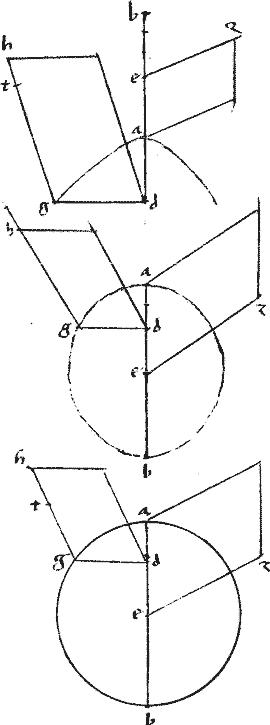
// Sed ae speciem az sicut de speciem⁴⁴ ex de similem⁴⁵ ipsi az. quandoquidem similium specierum⁴⁶ super iisdem lineis descriptorum eadem ratio⁴⁷.

// Igitur excessus, quo az species⁴⁸ superat dh speciem⁴⁹, aequale erit speciei⁵⁰, ex de simile ipsi az per 9^am 5ⁱ Euclidis quandoquidem ad dictum excessum, dictamque speciem⁵¹, [A:24r] ipsum de unam habet rationem.