Geometry, Algebra and Combinatorics of Moduli Spaces and Configurations VII

This is the 7th edition of the winter school held in Toblach in winter 2017, winter 2018, winter 2019, winter 2020, winter 2023 and winter 2024. There will be three 5 hours minicourses, some talks and ample time for discussion.

Mini-courses

• Giovanna Carnovale, Università di Padova, An introduction to Nichols algebras. (notes). [show abstract]

  Abstract: To any pair (V,c) consisting of a vector space V and a solution c ∈ GL(V ⊗ V) of the Yang-Baxter equation (c ⊗ id)(id ⊗ c)(c ⊗ id) =(id ⊗ c)(c ⊗ id)(id ⊗ c) one associates naturally an algebra, called Nichols (or shuffle) algebra. Nichols algebras are crucial for the classification program of Hopf algebras through the work of Andruskiewitsch, Angiono, Heckenberger, Schenider, Vendramin and their collaborators, and have had applications in the solution of Malle's conjecture in number theory by the work of Ellenberg, Tran and Westerland. Relevant but different algebras, such as the symmetric algebra, the exterior algebra, the positive part of quantized enveloping algebras, and Fomin-Kirillov algebras FK_3, FK_4 and FK_5 are examples of Nichols algebras. One of the basic questions is then how properties of (V,c) determine properties of the associated algebra, especially, for which pairs (V,c) is finite-dimensional, or finitely-generated. We will review some of the current and past approaches and solutions to this problem and mention two geometric interpretations of Nichols algebras, one, due to Meir, as elements in a close orbit for the action of a reductive group, and another, due to Kapranov and Schechtman, in terms of perverse sheaves on the space of complex monic polynomials.
  [Hide abstract]

• Fabrizio Catanese, Universität Bayreuth, Finite automorphism groups of complex and algebraic manifolds (notes1, notes2, notes3). [show abstract]

  Abstract:
  I) Automorphism groups of projective varieties and compact complex manifolds. Examples and the case of algebraic curves: the classical results of Hurwitz, Klein, Lefschetz.
  II) Finiteness criteria for Aut(X). Upper bounds for the cardinality |G|, for G a finite subgroup of Aut(X): the case where G is Abelian, or X is a hypersurface.
  III) Automorphisms with some type of topological triviality, in particular Aut_Q(X) = the group of automorphisms acting trivially on the rational cohomology of X, respectively Aut_Z(X) = the group acting trivially on the integral cohomology of X. The benchmark case of surfaces, according to the Kodaira dimension.
  [Hide abstract]

• Luis Ferroni, IAS Princeton, A gentle overview of Kazhdan-Lusztig-Stanley and Chow functions on posets (notes). [show abstract]

  Abstract: In 1992 Stanley noticed that certain special functions on posets called "kernels" give place to special polynomial functions. These are now known as Kazhdan-Lusztig-Stanley (KLS) functions, and depending on the choice of the poset and the kernel, give place to important objects in algebraic combinatorics. Three foundational examples are the following: i) when the poset is the Bruhat order of a Coxeter group and the kernel are the R-polynomials, the KLS functions are the famous Kazhdan-Lusztig polynomials; ii) when the poset is the face lattice of a polytope and the kernel is the map [F_1, F_2] \mapsto (x-1)^{\dim F_2 - \dim F_2}, the KLS function is the so-called toric g-polynomial of the polytope; and iii) when the poset is the lattice of flats of a hyperplane arrangement (or matroid), the KLS function is the Kazhdan-Lusztig polynomial of the arrangement. We will recapitulate these central notions, and compare it with a new kind of functions called "Chow functions", that I introduced in an on-going collaboration with Jacob P. Matherne and Lorenzo Vecchi.
  No prior knowledge about matroids, polytopes, or Coxeter groups is necessary, but having at least one of these examples in mind will be helpful.
  [Hide abstract]

Talks:

• Alessio D'Alì, Politecnico di Milano. Symmetry counts: an introduction to equivariant Hilbert and Ehrhart series. [show abstract]

  Abstract: The Ehrhart series of a lattice polytope P is a combinatorial gadget that counts the number of lattice points of P and of its dilations. The Hilbert series of a simplicial complex S counts how many monomials supported on faces of S exist in each possible degree. The aim of this talk is to introduce equivariant versions of such constructions, where we are not just interested in counting but we also want to record how the action of a finite group affects such collections of lattice points or monomials. Inspired by previous results by Betke-McMullen, Stembridge, Stapledon and Adams-Reiner, we will investigate which extra combinatorial features of the group action give rise to "nice" rational expressions of the equivariant Hilbert and Ehrhart series, and how the two are sometimes related. This is joint work with Emanuele Delucchi. [Hide abstract]




Train strike on Sunday February 23

It seems that this strike has been cancelled, so the train traffic should be normal on Sunday.




Train strike on Monday February 24

Be aware that a train strike by the local Trentino railway company is scheduled for Monday, February 24th. It is unclear whether the strike will be extended, but as a precaution, we are providing you with some travel information.
Local trains travelling between 6:00–10:00 AM and 6:00–9:00 PM will be guaranteed.
Local buses operating between 6:00–10:00 AM and noon–3:00 PM should also be guaranteed.
For further information, you can consult the official website (available in German and Italian).
Additionally, we would like to point out that buses to Dobbiaco may be available from major cities in the surrounding area. In particular, please note that line 402 buses from Brunico to San Candido stop in Dobbiaco.




Schedule


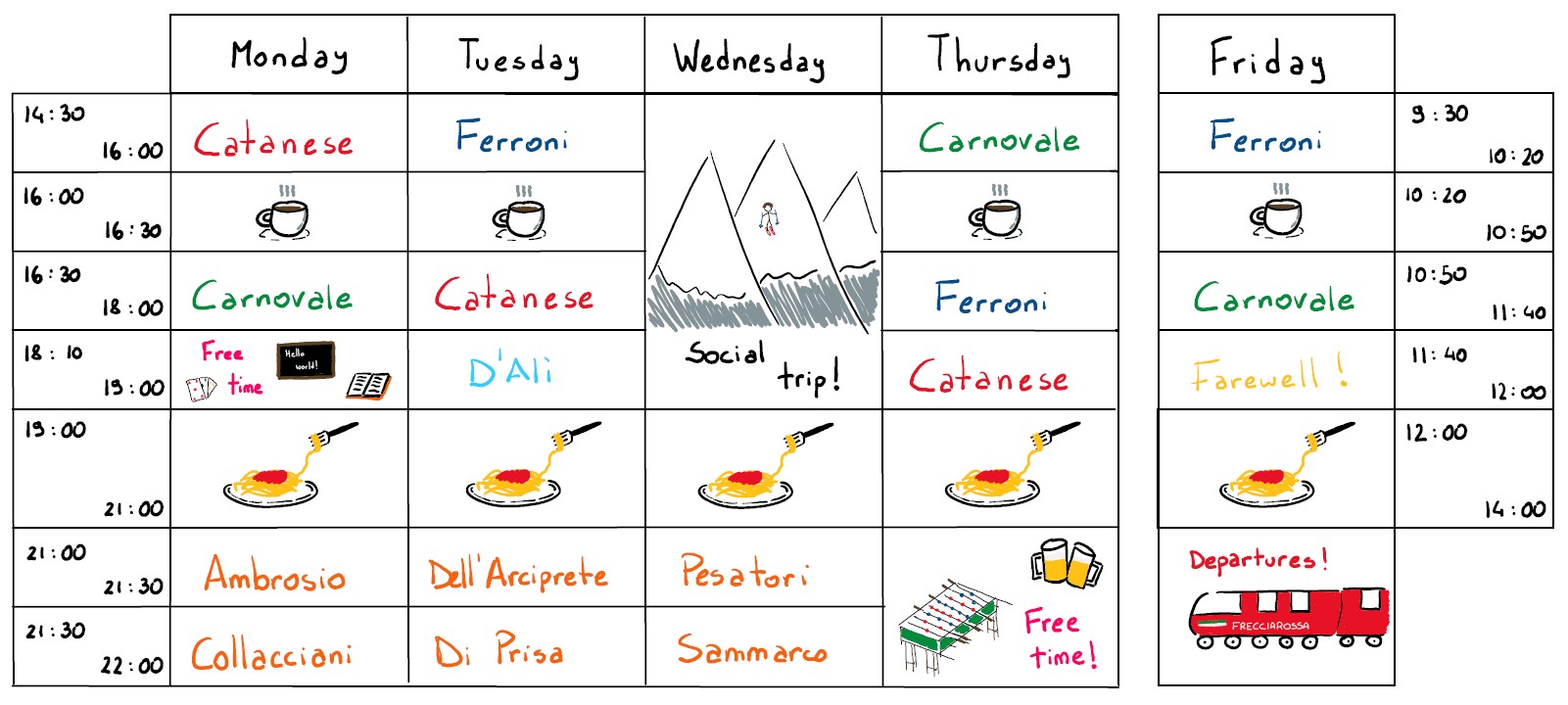
You can download a pdf with the schedule of the winter school here.


Participants:

• Davide Accadia, Università degli Studi di Trieste
• Filippo Ambrosio, Friedrich Schiller Universität Jena
• Alberto Avitabile, Università degli Studi di Roma - Tor Vergata
• Paolo Bravi, Università di Roma 'La Sapienza'
• Anna Bresciani, Università di Bologna
• Giovanna Carnovale, Università di Padova
• Fabrizio Catanese, Universität Bayreuth
• Fabrizio Caselli, Università di Bologna
• Elena Collacciani, Università di Padova
• Nirvana Coppola, Università di Padova
• Michele D'Adderio, Università di Pisa
• Alessio D'Alì, Politecnico di Milano
• Luca Da Col, Università degli studi di Trieste
• Luca Dal Molin, Università di Trento
• Alice Dell'Arciprete, University of York
• Alessio Di Prisa, Scuola Normale Superiore di Pisa
• Sabino Di Trani, Università di Roma 'La Sapienza'
• Mischa Elkner, Institute of Science and Technology Austria
• Tommaso Faustini, University of Warwick
• Alessandro Fenu, Università di Pisa
• Luis Ferroni, IAS Princeton
• Marco Franciosi, Università di Pisa
• Jacopo Gandini, Università di Bologna
• Lorenzo Giordani, Università di Bologna/Ruhr-University Bochum
• Sean Griffin, University of Vienna
• Daniel Holmes, Institute of Science and Technology Austria
• Giovanni Interdonato, Scuola Normale Superiore di Pisa
• Alessandro Iraci, Università di Pisa
• Dania Lazzarini, Università di Pisa
• Federico Lazzeri, Università di Pisa
• Lucrezia Beatrice Lorenzi, SISSA
• Alice Lotti, Università di Pisa
• Paola Malatacca, Università di Bologna
• Valerio Melani, Università di Firenze
• Luca Moci, Università di Bologna
• Luca Morstabilini, SISSA
• Vassilis Moustakas, Università di Pisa
• Nhok Tkhai Shon Ngo, Institute of Science and Technology Austria
• Lorenzo Noè, Università di Pisa
• Roberto Pagaria, Università di Bologna
• Giovanni Paolini, Università di Bologna
• Paolo Papi, Università di Roma 'La Sapienza'
• Lorenza Parisi, Università del Salento
• Lorenzo Perrone, Università di Bologna
• Simone Pesatori, Università di Roma Tre
• Tommaso Punis, Università di Pisa
• Menghao Qu, Scuola Normale Superiore di Pisa
• Roberto Riccardi, Scuola normale
• Noah Ruhland, Universität Bayreuth
• Mario Salvetti, Università di Pisa
• Elena Sammarco, Università di Roma Tre
• Alessio Sgubin, Università di Pisa
• Viola Siconolfi, Politecnico di Bari
• Matteo Tortolano, Università di Roma Tor Vergata
• Alejandro Vargas, University of Warwick
• Lorenzo Venturello, Università di Siena
• Cristofer Villani, Università di Pisa

Venue

The school will be held in Dobbiaco (Toblach) at the Kulturzentrum Grand Hotel Centro Culturale, in "La Sala degli Specchi". Kulturzentrum Grand Hotel Centro Culturale is located in front of Toblach train station (see the map).

Warning: there might be disruptions on the rail network thorugh Dobbiaco: check this link for more information.

Registration and support

Participants are required to register by filling in this registration form.
It would be very helpful for the organization if you fill in the form as soon as possible, thanks!

Limited funding will be available to cover local expenses (lodging, breakfast and dinner) of few Master or PhD students.
To apply for financial support you are required to fill in the same form.
The deadline to apply for funding is December 8, 2024.
Again, we encourage to apply as soon as possible in order to help the organization, thanks!

For any question, you can contact the organizers at the following email address: toblachconfigurations@gmail.com.

This workshop is supported by:

MUR, Dipartimento di eccellenza, University of Pisa.

Instituto Nazionale Di Alta Matematica INDAM.

GNSAGA, INDAM.

PRIN 2022, ALgebraic and TOPological combinatorics (ALTOP).

Progetto di Ateneo 2023 Teoria delle rappresentazioni e applicazioni, University "La Sapienza" of Rome.

Organizers: Michele D'Adderio , Sabino Di Trani , Marco Franciosi , Alessandro Iraci and Paolo Papi.