1 Theorema XXVII

Latitudo colorum iridis sub eum fere angulum ab oculo comprehenditur, sub quem et solaris corporis diameter.

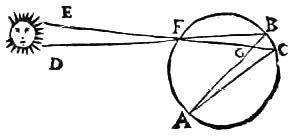
Sit¹ centrum visus a, angulus autem, sub quo iridis latitudo comprehenditur, bac. Profluentibus² a sole extremis radiis db et ec se in signo f secantibus, eritque angulorum fba et fca uterque recti 1/2 per 25^am3. 2 Sed fgb ipsi angulo agc sibi contraposito⁴ aequalis. Ergo reliquus bfc reliquo bac⁵ aequalis. Sed [S:53] ipse efd ipsi⁶ bfc contraposito⁷ aequalis. Igitur et bac angulus sub quo latitudo colorum iridis cernitur aequalis est ipsi efd⁸ sub quo solaris diametri latitudo spectatur. 3 Si enim ipsi triangulo abc circulus circumscribatur, idem circulus triangulum fbc⁹ circum[C:41v]scribet¹⁰, qui quidem circulus insensibilis est magnitudinis respectu solaris distantiae. Quam ob rem¹¹ angulus efd insensibiliter differet¹² ab angulo quem¹³ solis diameter oculo a subtendit.

4 Corollarium¹⁴

Si ergo sol propinquior esset, iris sub maiore¹⁵ latitudinis angulo appareret. Accendente¹⁶ enim sole,¹⁷ angulus efd, et¹⁸ ideo angulus bfc, et ideo angulus bac maior fit¹⁹.

5 Aliud²⁰

Idem sequitur, quo locus iridis remotior fit²¹. Crescente enim distantia ab, crescit circulus fbc, et ideo angulus efd, et per consequens bac angulus maior fit. [C:42r]