24

84 Age nunc scrutemur et⁶¹ dodecahedri⁶² angulum. Sed in hoc solido et item in icosahedro, linea quae angulum subtendit, non habet ad utrumlibet anguli brachium proportionem⁶³ rationalem vel longitudine [A:8r]vel saltem potentia: sciscitabimur igitur hoc per calcumum numeralem ut quatenus erit necessarium, vero appropinquemus.

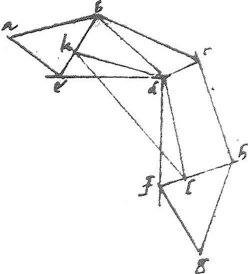
Sumo itaque geminas dodecahedri bases contiguas abcde et cdfgh latus cd commune habentes, mox protraho rectas be, fh ad quas perpendiculares⁶⁴ duco a puncto d, dk quidem ad be, dl autem ad fh. 85 Et quoniam tam be quam fh ipsi cd parallelus est, ideo per 29^am primi ipsae dk, df ad ipsam cd rectae sunt, angulus ergo kdl erit is, quem duo dodecahedri plana comprehendunt. Supponatur itaque be vel fh partium 1000000 quo numero prope verum secto secundum mediam extremamque rationem erit maius segmentum maius quidem 618033, minus vero quam 618034. Tanta autem erit ed si 11^am 13ⁱ bene inspicias, latus scilicet ipsius dodecahedri. Connexaque bd aequali ipsi be, cuius quadratum qd est 1000000000000. 86 Subtrahatur a quadratis ipsarum be, ed, et supererit quadratum ed, quod erit maius quam partes 381964789089, minus vero quam 381966025156 tantum est autem id, quod ex duplo ipsius be in ek fit, si 13 ^ae secundi credimus. Secetur igitur illud in duplum ipsius be, hoc est in 2000000, et ex divisione subsilient maius quidem quam 190982789089/2000000, minus vero quam 19098325156/2000000, et tanta erit ek et a fortiori ipsa ek maior erit quam 19098239/100, minor vero quam 1909833/200. Quare quadratum ek si recte numeres, maius est quam 36474273289, minus vero quam 36474512019. 87 Utrumque horum numerorum subtraho ab utroque numero quadratum ed claudente, minorem scilicet horum a maiori illorum, et maiorem horum a minori illorum: sic enim supererit quadratum ipsius kd maius quidem quam 345490277070 minus vero quam 345491751867. Sed quadratum kl est partium 1000000000000 quoniam scilicet kl ipsi ef aequalis est propter aequidistantiam linearum ek, lf et ipsa ef ipsi eb aequalis est, quae supposita fuit partium 100000. Habes igitur prope verum magnitudinem anguli kdl qua mox conferendo utemur.