17

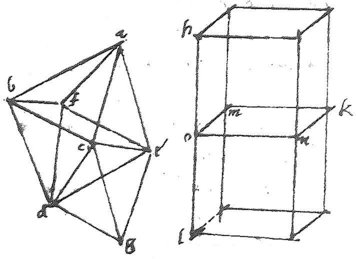
65 Restat nunc angularem congruentiam pyramidis, octahedri et duorum cuborum depingere, ne quid non depictum remaneat. Sit itaque octahedrum abcdef cuius basium uni, utpote basi dce congruat una basium pyramidis, quae sit dceg, ita videlicet ut basis dce sit communis octahedri et pyramidis, ex qua coniunctione hoc sequitur, ut unaquaeque trium reliquarum basium pyramidis, quae sunt cdg, deg, ecg cum unaquaeque basium octahedri sibi contermina unum componant planum, ut scilicet bcd⁴⁸ basis octahedri cum cdg basi pyramidis sit unum planum. 66 Itemque fde basis octahedri cum deg basi pyramidis unum sit planum, nec non aec basis octahedri cum ecg basi pyramidis unum sit planum. Quod quidem demonstratur, immo apertissime patet ex praecedenti capite: nam quod in praecedenti descriptione facit una pyramidum⁴⁹ aegl, begf, cfgh, dhkl cum octahedro eh idem in praesenti facit pyramis cdge cum octahedro ad exempli gratia, sicut in praecedenti figura unusquisque trium rhomborum af, ah, ak in uno iacet plano, quandoquidem sunt in tribus basibus pyramidis abcd. Sit in praesenti quilibet trium rhomborum ag, bg, fg unum est planum. 67 Coniungantur itaque duo cubi hk kl ad communem basim mn quo fiet ut quaelibet quatuor basium cubi hk erecta super basim mn sit in rectum coniuncta basi cubi kl sibi conterminae, exempli gratia, ut hm basis⁵⁰ directe coniuncta basi ml unum cum ea faciens planum, quod manifeste patet ex congruentia cuborum in 14^ocapite. 68 Sit ergo unus ex tribus rhombis ag, bg, fg utpote rhombus ag superponatur plano hml, ita ut totus rhombus ag iaceat in plano hml, congruentibus etiam rectis ce, mo in unum. Iam haec quatuor solida videlicet pyramis cdge octahedrum ad cubi duo hk, kl angulariter locum implebunt: nam quatuor ipsorum angularia latera ad unam rectam ce vel mo⁵¹ quae in unam coëunt, ita concurrunt, ut nihil vacui supersit. Et hoc erat nobis lineari descriptione patefaciendum.