IX. Si in quolibet cono triangulum per axim rectum sit ad basim, plana vero ad triangulum recta, faciam hyperbolas quatuor; primam, cuius diameter aequidistet lineae descendenti ab angulo trianguli, qui apud verticem ad basim, et angulum per medium secanti; secundam, et tertiam, quarum diametri aequidistent lineis ab eodem angulo deductis, et angulos aequales hinc, et inde cum prima descendente suscipientibus; quartam, cuius diameter aequidistet lineae a dicto angulo delapsae, ac remotiori a prima descendente. Tunc in prima hyperbola transversa diameter ad rectam habebit minimam rationem; in secunda, et tertia eamdem omnino, et minorem quam in quarta.

In cono abg, cuius vertex b; basis circulus amg, triangulum ad rectos basi sint abg, quam or autem plana recta ad triangulum, faciant quatuor hyperbolas; primam kml, cuius diameter kl, aequidistet ipsi bd, secanti bisariam, angulum abg; secundam, et tertiam kxn, rys, quarum diametri kn, rs aequidistent ipsis be, bz, suscipientibus utrinque angulos aequales cum ipsa bd; quartam denique kpo, cuius diameter ko, aequidistet ipsi bh; quae remotior est ab ipsa bd media, quam be, vel b.

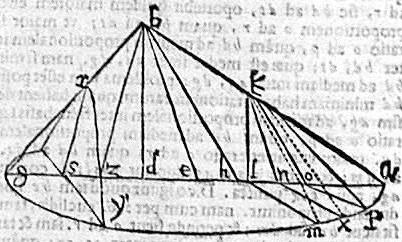
Tunc aio quod in hyperbola km transversa diameter ad recta minor est ratio quam in hyperbolis kx, ry; et in ipsis hyperbolis kx, ry, transversa ad rectam eamdem pariat rationem, et minorem, quam in hyperbola kp. Namque per 12. p. conicorum, in hyperbola km transversa ad rectam est, sicut quadratum bd ad rectangulum adg; in hyperbola kx est sicut quadratum be ad rectangulum aeg, in hyperbola ry, sicut quadratum bz ad rectangulum dzg, in hyperbola kp, sicut quadratum bh ad rectangulum abg. Sed per 7. huius eiusque corollarium [S:177] quadrati bd ad rectangulum aeg minor est proportio, quam quadrati bz ad rectangulum aeg; et quam quadrati bz ad rectangulum azg. Ipsum vero quadratum be ad rectangulum aez, est sicut quadratum bz ad rectangulum azg. Et ipsum quadratum be ad rectangulum aeg, vel quadratum bz ad rectangulum azg minorem rationem habet, quam quadratum ab ad rectangulum abg. igitur in hyperbola km transversae ad rectam minor proportio est, quam in hyperbolis kx, ry; et in his eamdem habet rationem, et minorem quam in hyperbola kp, quemadmodum demonstrandum proponitur. Unde manifestum est quod hyperbola, cuius diameter cum latere trianguli per axem suscipit dimidium anguli verticalis amplissima est; cuius vero diameter minorem cum latere trianguli suscipit angulum angustior est; similes porro hyperbolae sunt quarum diametri cum lateribus trianguli aequales suscipiunt angulos. Voco autem ampliorem hyperbolam cuius transversa minorem ad rectam diametrum habet proportionem; angustiorem autem; cuius maior.