X. Datum conum plano secare, ut sectio sit hyperbole similis data hyperbole.

Esto datus conus abg, cuius vertex b; basis amg circulus; triangulum per axem ad rectos basi abg; data hyperbole de, cuius transversa ze; recta vero eh.

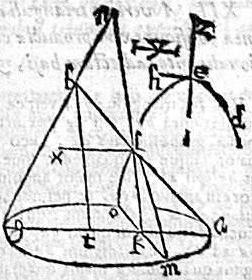
oportet secare conum abg plano ea lege, ut sectio sit hyperbole similis ipsi hyperbo lae de. Sit per 9. 6. Euclidis, linea y media proportionalis inter ipsas ze, eh; et per 8. praecedentem, in triangulo abg ducatur ab angulo b linea bt, quae ad mediam proportionalem inter at, tg sit, sicut ze ad y. Unde necesse erit ut ratio ze ad y non minor sit, quam ratio lineae descendentis ab angulo abg, ipsumque; bisariam secantis, ad me diam proportionalem inter facta basis ag segmenta, ut in 8, ostensum est. Sic enim fiet ut ze ad eh, sic quadratum bt ad quadratum dictae mediae proportionalis, hoc est rectangulum atg, quod et fieri poterit, scholium 8, ut scilicet sit sicut ze ad eh, sic quadratum bt ad atg re ctangulum. Quo facto ducatur in triangulo abg linea kl aequidistans ipsi bt; et producta coincidat lateri gb producto apud n. item km ad rectos ipsi ag; et extandatur planum in quo iacent lineae lk, km, faciens in cono sectionem mlo. Quam dico hyperbolen esse ipsi de hy- perbolae similem. Quod enim sit hyperbole patet, per 12. 1. conicorum. Sit ergo sicut quadratum bt ad rectangulum atg, hoc est sicut ze ad eh, sic nl ad lx. Eruntque per dictam 12. , nl, lx transversa, et recta Dyametri hyperboles lmo. Itaque hyperbolarum de, ml transversae ze, ln proportionales sunt rectis eh, lx. Igitur per 3 huius, similes sunt hyperbolae de, ml. Ergo datum conum abg plano sic secavimus, ut sectio iam mlo hyperbole sit similis datae hyperbolae de. Sit hoc proponebatur faciendum.