III. Hyperbolae quarum transversae rectis diametris sunt proportionales: sunt inter se similes. Et e contrario similium hyperbolarum proportionales sunt transversae rectis diametris.

Sint duae hyperbolae ab, de, quarum transversae ag, dz sint rectis diametris ah, dt proportionales.

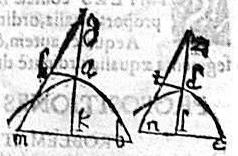
Aio quod similes sunt ab, de hyperbolae. Copiantur enim ex axibus segmenta ak, dl diametris ipsis proportionalia; et ordinate ducantur bk, el; et producantur ut ipsis gh, zt coniunctis, productique coincidant ad m, n puncta. Itaque ex hypothesi, si et sicut ak ad dl, sic iam km ad ln. Similia igitur erunt rectangula akm, dln; et ideo sicut ipsarum ak ad dl duplicata; et ideo sicut ipsarum ag ad dz ratio duplicata. Sed per 12.p. conicorum, quadratum bk aequum est rectangulo akm: et per eandem quadratum el aequum rectangulo dln. Item quadratorum bk, el ratio erit, et ipsarum bk ad el duplicata. Aequales igitur sunt hae rationes duplicatae: quandoquidem tetragona quadratis aequalia. Ergo et ipsae rationes aequales, hoc est bk ad el, sicut ak, ad dl. Quo sit, ut cum in conicis sectionibus ab, ed ipsa axium segmenta ak, dl diametris proportionalia, suscipiant ipsas bk, el ordinatas, sibi proportionales. Idque ipsum eveniat, simili argumento in quibuscunque axium segmentis, ad diametrorum rationem assumptis. Iam per diffinitionem similes sunt ab, ed sectiones. Quod erat demonstrandum. Conversaque haud difficilius ostendetur ex hyperbola, et aequa proportione.

Unde constat hyperbolas, quarum transversae aequales, et rectae aequales, esse quod: inter se similes, et aequales. Namque ex aequalitate diametrorum sequi aequalitatem tetragonarum superficierum, quas potiunt ordinatae, et perinde ipsarum ordinatarum aequalitatem; et per diffinitionem sectiones similes, et aequales esse, et e contrario.