XVII. Iisdem suppositis; utque prius posita eadem recta diametro ellipsis, et paraboles: demonstrandum est quod talis ellipsis est maxima ellipsium circa eumdem axem descriptarum, et intrinsecus parabolam talem tangentium. Et vicissim quod parabola talis est minima parabolarum extrinsecus ellipsim talem tangentium.

Iisdem subiectis. Ponatur ut in ante praemissa ellipsis eb, habens rectam bg; quae et paraboles recta est.

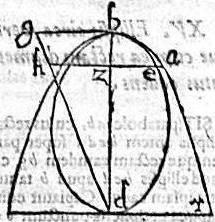
Aio iam quod eb ellipsis est maxima inter ellipses circa bd axim descriptas, et intus tangentes parabolam ab. Contra autem quod parabola ab minima est inter parabolas extrinsecus tangentes ellipsim be. Nam cum per 15.huius, ellipsis eb tota intus existens. Tangat parabolen ab; atque per primam huius, eiusque corollarium, infinitae ellipses circa axem bd positae tangant ellipsim be; et perinde parabolam ba: atque demum per praecedentem, cum quaevis ellipsis circa bd diametrum descripta, et habens maiorem rectam quam bg secet ipsam parabolen iam ex his illud sequitur, ut ellipsis eb sit maxima inter ellipses circa bd diametrum descriptas. Et intus tangentes parabolen ab: hoc est maximam inter eas rectam diametrum habet. Rursus autem quoniam per 15.huius, parabola ab vicissim extrinsecus cadens, tangit eb ellipsim, et per primam huius, eiusque corollarium infinitae parabolae ipsam eb ellipsim extrinsecus tangunt, tangentes videlicet parabolam ab: etper praecedentem, quaevis parabole habens rectam diametrum minorem recta ellipsis, secat ipsam ellipsim; idcirco sequitur ut parabola ab sit minima inter parabolas extra ellipsim eb tangentes, hoc est minimam inter eas rectam diametrum habet. Et hoc est quod proponebatur demonstrandum.

Notandum, et hic, quod cum prima pars praesentis 17, intelligatur de ellipsibus circa axem bd positis. Iam si capiatur ellipsis habens axim maiorem quam bd, ipsamque rectam diametrum bg. Tunc talis ellipsis per praesentem 17. vel 15, intra quidem parabolam ab;per primam huius, eiusque scholium, extra ellipsim eb cadet. Unde quamvis inter parabolam ab, et ellipsim be, neque ellipsis ulla circa axem bd posita; neque ulla parabole intercidat, ut ex demonstratione praesentis patet. Tamen inter easdem infinitae ellipses habentes azem maiorem quam bd; et rectam ipsam bg intercidere possunt, sicut scholium inferebat.

Praeterea sciendum, quod iisdem suppositis; posita videlicet recta ellipsis, sive circuli, ut in 15. et 3. huius, et recta paraboles una, et eadem. Tunc in parabola linea, quae ordinate ducitur ad extremum diametri transversae ellipsis, sive circuli. Hoc est ipsa rd, aequalis est 3, diametro ellipsis, vel circuli. Namque rd per 11. p.Conicorum, potest rectangulum dbg. Et per 13. eiusdem, secunda diameter ellipsis, vel circuli potest idem rectangulum dbg, speciem videlicet, quae adiacet ad primam [S:163] diametrum, quare iam dicta linea rd, et secunda diametros sunt aequales.