XVI. Eisdem suppositis, si ellipseos diameter recta ponatur maior, quam recta paraboles: tunc ellipsis parabolen in vertice tangens, et excedens eam utrinque secabit.

Iisdem manentibus. Ponatur be recta ellipsis amb, maior quam bg recta paraboles.

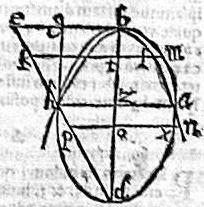
Dico tunc quod ellipsis excedes secat parabolem. Ducatur enim axi bd aequidistans gh, incidens ipsi de apud b punctum, per quod agatur ordinate bza in parabola. Erit auten zh aequalis ipsi bg; sed in parabola per 11.1, Conicorum, az poterit rectangulum gbz, et per 13, in ellipsi ordinate ducta a puncto z poterit rectangulum bzh, aequale ipsi rectangulo gbz. Igitur ordinate ducta in ellipsi est ipsa za, et perinde punctum a est in utraque periferia. Secant ergo se peripheriae in a puncto. Mox per punctum m in ellipsi inter a, b ordinate agatur, ut in 4. huius, mltk. Et tunc in ellipsi linea mt poterit rectangulum btk: in parabola vero lt poterit rectangulum gbt, minus, et ideo lt brevior, quam tm. Sit ut arcus [S:162] ellipsis amb arguatur parabolen. Demum per punctum x sub a, in ellipsi relictum, ordinate agatur, in ut 4.huius, nxop. Et tunc in ellipsi linea xo poterit rectangulum bop; atque in parabola na poterit rectangulum gbo, maius rectangulo bop. Et ideo no longior quam xo. Unde arguetur peripheria ellipsis axd, reliqua intra parabolen. Et hoc idem demonstrabimus in peripheriis ad reliquas axis partes. Quemadmodum proponitur demonstrandum.