XV. Ellipsis circa verticem, aximque paraboles constituta eamdemque cum ea rectam diametrum habens: in solo vertice parabolen tangit, intus cadens.

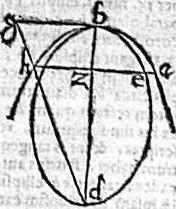
Sit parabole ab, cuius recta diametros bg, axis bd; ellipsis autem bed, super partem axis posita bd, habensque rectam eamdem bg cum parabola. Aio iam quod ellipsis bed apud b tantum tangens parabolam intra ipsam cadit. Capiatur enim ut cunque relictum in elliptica peripheria punctum e, per quod ordinate ducatur aezh, coincidens parabolae, axi, lineaeque gd apud ipsa a, z, h puncta. Et tunc per 11. primi conicorum, az poterit rectangulum gbz. Ipsa vero ez poterit rectangulum bzh, minus ipso rectangulo gbz, quare brevior est ez, quam az; et perinde punctum e in peripheria ellipsis, et omne aliud punctum, ipsaque peripheria tota, intra parabolam cadit, eam apud b tantum tangens nec refert virum bd, sit maior, minorve axium ellipsis. Quod fuit demonstrandum.