XIV. Eisdem supposiris, si ut antea circuli diameter ponatur aequalis rectae diametro ellipsis, quae minori axe adiacet: demonstrandum est quod talis circulus est minimus circulorum talem ellipsim extrinsecus tangentium. Contra vero quod talis ellipsis est maxima ellipsium super dictum axem positarum; et intrinsecus circulum tangentium; hoc est inter ellipses super illum axem positas, est illa, quae maximam rectam diametrum sortitur.
Iisdem suppositis. Ponatur ut in antepraemissa circuli diameter be, aequalis ipsi bd, ellipticae rectae.
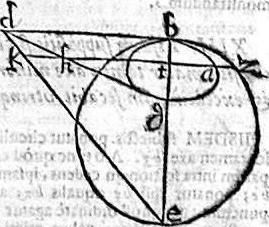
Demonstrandum est quod circulus bze est minimus circulorum ellipsim ab extrinsecus tangentium contraque quod ellipsis ab est maxima inter ellipses super axim bg descriptas, et intrinsecus bze circulum tangentes; hoc est maximam inter eas rectam diametrum habet. Nam cum per 11. huius, circulus bze totus extra ellipsim cadat, tangens eam apud b; cumque per primam huius, eiusque corollarium, infiniti circuli tangant exterius ipsum bze circulum; et perinde ipsam ab ellipsim apud b. Cum denique per praecedentem, omnis circulus, cuius diameter minor sit ipsa bd secet ellipsim, aliquatenus inter eam intercedens. Ex his iam sequitur circulum bze minimum esse circulorum super dicto axe centrum habentium, et ellipsim ab extrinsecus tangentium. Rursus quoniam per 12. praemissam, ellipsis ab intra circulum bze cadens ipsum apud b punctum tangit; atque per primam huius, eiusque corollarium, infinitae ellipses circa axim bg, intus apud b tangunt ellipsim et circulum. Ac demum per praecedentem, posita ellipsis recta bd, maiore quam be circuli diametro, tunc ellipsis flectitur partim circa circulum, propterea ex his sequitur ellipsim ab maximam esse ellipsium circa bg axem positarum, et intus circulum bze tangentium; hoc est maximam inter eas rectam sortiri. Quod iam restabat demonstrandum.
[S:161]
Notandum quod 2. pars praesentis 14. propositionis intelligitur de ellipsibus super axim bg descriptis, quod si capaitur ellipsis, cuius axis minor a puncto b ceptus inter puncta g, e desinat, habens tamen rectam axi adiacentem bd. Tunc talis ellipsis (ex hac 14. vel 12) circulum bze tangens apud b, intra ipsum cadet, per primam autem huius, eiusque scholium, extra ellipsim ab feretur. Unde quamvis inter ellipsim ab, circulumque bze (per primam partem huius 14) circulus non intersit, nec ulla ellipsis habens axim bg (ut per 2.partem huius) patet. Itemque nec aliqua ellipsis habens axem maiorem quam bg, recatmque minorem, maioremve, quam bd (ut constat per 13. huius, perque scholium primae huius) tamen inter ipsas ab ellipsis, circulique bze peripherias, intercidere possunt infinitae ellipses; quarum omnium recta diametros sit ipsa bd, axesque a puncto b cepti, inter g, e puncta desinant: sicut scholium insert. Nunc videamus quemadmodum ellipsis tangendo, secandoque parabolae coniungatur.