XIII. Eisdem suppositis, si circuli diameter ponatur minor quam recta ellipsis, maior tamen axe minori: tunc circulus ellipsim ibidem tangens, et excedens, eam secabit utrinque.

Iisdem subiectis. Ponatur circuli diametros be, minor quam recta ellipsis bd, maior tamen axe bg. Aio tunc quod circulus bae tangens ut ante, ellipsim apud b, partim intra sectionem cadens, ipsam utrinque secabit. Nam cum bd sit maior quam be; ponatur ipsi he aequalis bz; atque ipsae zd, ez, coniunctae secent se apud b punctum; per quod ordinate agatur bta, incidens axi apud t, ellipsi vero apud a punctum. Unde per 13. vel 15. primi Conicorum, in ellipsi linea a: poterit rectangulum bth; in circulo autem ordinata ad t punctum, poterit rectangulum bte. Hoc est ipsum rectangulum bth, quo sit ut talis ordinata in circulo sit ipsamet ta; ipsumque a punctum sit in peripheria circuli: et perinde circulus. Et ellipsis in ipso a puncto se invicem secent. Arcus autem circuli bla intra sectionem cadet. Capiatur enim [S:160] in peripheria ellipsis inter a, b puncta quodvis relictum punctum k, a quo ducatur ordinate klmxn.

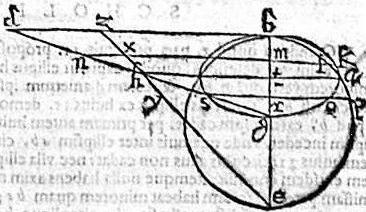
Coincidens circulo, axi, et ipsis gd, ez, apud ipsa l, m, x, n. Et tunc per 13. vel 15. Conicorum, in ellipsi km poterit rectangulum bmn; in circulo autem lm poterit rectangulum bmx, quod est ipso rectangulo bmn minus. Atque adeo brevior erit lm, quam km. Unde punctum l, et similiter omnia puncta arcus circuli bla, et ipse arcus totus, intra ellipsim cadit. Sub puncto autem a circulus extra ellipsim fertur, quod assumpto in peripheria ellipsis o puncto: per que illud ordinate ducta porsy, patebit. Nam in ellipsi or poterit rectangulum brs; in circulo pr poterit rectangulum bry, maius. Et ideo pr longior quam ro, quare, etc. Patet ergo veritas eius, quod proponitur demonstrandum.