XII. Circulus ad verticem minor axium ellipsis, super ipsum axem positus, habens diametrum aequalem recte diametro eiusdem ellipsis: in vertice tangit sectiomem, totus extra ipsam cadens.

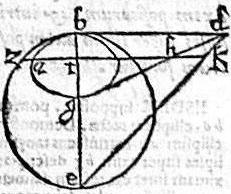
Sit ellipsis ab, cuius minor axis bg; et recta diametros bd; cui aequalis producta ponatur be, super qua circulus describatur bze. Aio quod circulus bze ellipsim ab, apud b tantum tangens, totus extra sectionem cadit. Capiatur enim in peripheria ellipsis quodvis relictum punctum a; per quod ordinate agatur zathk, coincidens circulo, axi, lineisque; gd, de apud z, t, h, k puncta et tunc per 13. vel 15.1. Conicorum, in ellipsi quidem at poterit rectangulum bth: in circulo autem zt poterit rectangulum bte, quod est ipsum rectangulum btk, maius rectangulo bth, longior ergo zt, quam ta, et ideo punctum a intra circulum est. Similiter autem ostendam quod omnis puncta ellipseos peripheriae; et perinde tota peripheria ellipsi intra circulum continetur, quare circulus bze ellipsim apud b duntaxat contingens, totus extra ellipsim cadit. Quod erat demonstrandum.