VIII. Eisdem suppositis; utque prius positis circuli diametro, et recta hyperboles aequalibus: demonstrandum est quod talis circulus est maximus circulorum intus hyperbolen, apud verticem tangentium. Atque vicissim quod talis hyperbole est minima minimam rectam diametrum habens, tangentium apud verticem hyperbolarum sub eadem transversa.

Iisdem subiectis; positis ut in sexta praemissa be circuli diametro, atque bd recta hyperboles aequalibus.

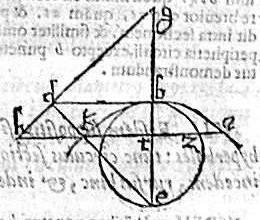
Aio quod circulus bze est maximus circulorum intrinsecus hyperbolem apud b verticem tangentium. Quodque ab hyperbole est minima hyperbolarum tangentium extra circulum apud eumdem verticem. Nam cum per ante praemissam circulus be, totus intra sectionem, tangat eam apud b; atque per primam huius, eiusque corollarium, infiniti circuli super lineam be tangant intus be circulum. Et perinde ipsam ab hyperbolen, ac demum per praecedentem, posito circuli diametro maiore quam bd, circulus ipse eccedet hyperbolen. Idcirco sequitur circulum be maximum esse circulorum intus tangentium hyperbolen ab, quod est primum ex propositis. Rursus quoniam per ante praemissam, hyperbola ab circulum eb extra tangens apud b, tota extra circulum incedit. Cumque per primam huius, eiusque corollarium, atque etiam per 2. huius, infinitae hyperbolae extra tangant ipsam hyperbolam [S:157] ab, et perinde ipsum circulum be. Itemque per praecedentem si ponatur hyperbolae recta diameter bd minor diametro circuli be. Iam tunc hyperbola cadet intra circulum, propterea ex his sequitur hyperbolen ab minima esse. Hoc est infimam, sive minimam rectam diametrum sortiri inter hyperbolas, sub eadem transversa extrinsecus tangentes circulum be. Quod fuit demonstrandum.

Notandum in praesenti theoremate quod hyperbole ab inter hyperbolas extrinsecus tangentes circulum be, et habentes transversam diametrum bg. Est illa, quae minimam rectam diametrum habet; ipsam scilicet bd. Nam omnis hyperbole habens transversam bg, et rectam diametrum minorem bd, cadit per aliquem arcum intra circulum: quemadmodum 2. pars propositionis sonat. Et inde fuit demonstratum quod si sumatur super eundem axim, hyperbole habens transversam diametrum maiorem quam bg; atque rectam diametrum ipsam bd. Tunc ex huius et demonstratione, talis hyperbole tanget circulum apud b; et extra ipsum cadet. Per 3. autem huius, intra ab hyperbolen cadet intrinsecus ipsam in dicto puncto tangens. Unde quamvis inter peripherias hyperboles ab, circulique be. (ut per 1. huius 8. partem constat) Circulum alium, cadere sit impossibile: itemque inter easdem peripherias nulla hyperbola cadere possit, habens transversam bg (ut 2. pars huius 8, concludit) nulla item hyperbola habens rectam minorem bd (ut in 7, praecedenti fuit ostensum) nulla demum hyperbole habens rectam bd, vel maiorem, ac transversam minorem quam bg, (ut 2. huius ratiocinatur). Tamen inter easdem peripherias hyperboles ab, circulique be intercidere possint infinitae hyperbole, habenyes scilicet transversam maiorem bg, atque rectam diametrum bd. Itaque satis discussa est speculatio circa hyperboles, atque circuli sese in vertice tangentium collationem. Transcundum nunc (ut ordo postulat) ad ellipsis, et circuli contactum.