III. Circulus habens eundem axim, ac verticem cum parabolae, diametrumque ipsius rectae aequalem: in solo vertice sectionem tangens, totus intra eam cadit.

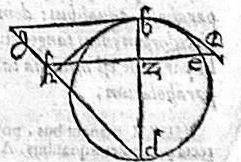
Sit parabole ab, cuius recta diametros bg, axis bd, de quo ipsi bg aequalis suscipiatur bd; super qua diametro circulus describatur bed. Aio iam quod circulus bed parabolam in solo b vertice tangit; totusque intra eam cadit. Capiatur enim in peripheria paraboles ut cunque relictum punctum a; et ordinate ducatur aezh; axi apud z, ipsique gd coniunctae, apud b, coincidens. Et manifestum erit, per 11.1. Conicorum, quod az poterit rectangulum gbz, at ez [S:154] potest bzd; quod est rectangulum bzk. Maius autem est rectangulum gbz, quam rectangulum bzh. Igitur az longior quam ez, et perinde punctum a extra circulum cadit; et punctum e intra parabolam, itaque excepto puncto b contactus, totus circulus intra sectionem cadet. Sicut proponitur demonstrandum.