II. Duarum hyperbolarum circa eumdem axim, eumdemque verticem descriptarum, et eamdem rectam diametrum habentium; quae minorem transversam habet in ipso tantum vertice tangit reliquam exterius incidens.

Sit hyperbola ab, habens transversam bg; rectamque bd. Item hyperbola eb, habens transversam bz maiorem ipsa bg; et rectam eandem bd.

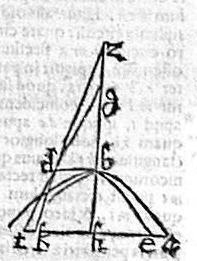
Aio quod hyperbole ab, ipsam eb, in solo b vertice tangens, extra eam incedit. Capiatur enim in peripheria ab punctum quodvis a; et ordinate ducatur aehkt, coincidens reliquae peripheriae apud e; axique apud h; ipsisque gd, zd coniunctis, ac productis apud k, t puncta. Et tunc per 12.primi conicorum, ah poterit rectangulum bht; ipsa vero eh poterit rectangulum bhk. Unde sicut in praemissis arguetur ah maior quam eh, et ideo punctum a extra sectionem eb; et similiter omnia puncta peripheriae ab; et perinde ipsa peripheria tota, extra sectionem eb, excepto ipso puncto b verticis, contactusque. Sicut fuit demonstrandum.

Quod si ponatur hyperbole ab habere rectam diametrum maiorem ipsa bd, non minus idipsum sequeretur, quod demonstratum est. Et similiter infinitae hyperbolae deduci possent intus, et extra ipsam ab, in solo b vertice ipsam, seque invicem tangentes.