IV. Eisdem suppositis, si circuli diameter ponatur maior, quam recta paraboles: tunc circulus sectionem in vertice tangens, partimque extra ipsam, partim intra cadens, in duobus eam locis secabit.

Iisdem manentibus ponatur bd diameter maior, quam bg recta paraboles. Aio tunc quod bad circulus tanget parabolam in puncto b; et inde utrinque extra flexo ambitu hinc, et inde secabit parabolen: nam cum bd maior sit quam bg, producatur bg, ponaturque ipsi bd aequalis bz; et coniucta de, sit ipsi bg aequalis dz; et per punctum z ordinate ducatur ad peripheriam paraboles azk, occurrens ipsi de apud b. Dico itaque quod circulus in ipso puncto a secat parabolen. Cum enim triangulum abd sit isosceles, erit et triangulum dzh isosceles, hoc est bz latus aequale lateri zd. Fuit atem zd aequalia ipsi bg. Ergo et bg aequalis zh, et perinde rectangulum gbz aequale rectangulo bzh. Per 11. autem 1. Conicorum, ordinate ducta in parabola ad punctum z. Hoc est ipsa az potest rectangulum gbz; et ordinate ducta in circulo ad punctum z potest rectangulum bzd; quod est ipsum rectangulum bzh. Igitur talis ordinate ducta aequalis est ipsi za. Et ideo punctum a est in peripheria circuli, quare circulus, et parabola se invicem secant in puncto a.

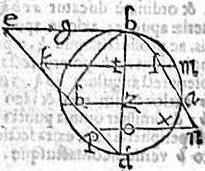
Arcus vero circuli bma flectitur extra parabolam; quod sic ostendam. Capiatur in parabola punctum quod libet inter a, b puncta, quod sit l, per quod ordinate ducatur mltk, coincidens circulo apud m, diametro apud t, ipsique de apud k. Et quoniam tk longior quam zh, ideo longior erit, et quam bg, quare rectangulum btk maius quam gbt. Sed per 11.1 Conicorum, lt potest rectangulum gb; et in circulo, mt potest rectangulum btk. Igitur lt brevior erit, quam mt, et ideo punctum m in peripheria circuli est extra parabolen, et similiter ostendam quod omnia puncta peripheriae circularis bma; atque totus omnino arcus bma cadit extra sectionem bla. Sub puncto autem a peripheria paraboles cadit extra circulum. Capiatur enim in peripheria paraboles quodvis punctum n; per quod ordinate ducatur nxop; circulo axi, et lineae de occurrens apud x, o, p puncta. Et quoniam op brevior quam zh; et ideo quam bg. Ideo maius erit rectangulum gbo, quam rectangulum bop. Sed per 11.1 Conicorum, no potest rectangulum gbo, et in circulo, xo potest rectangulum bod; quod est rectangulum bop. Longior ergo no, quam xo, et ideo punctum n in parabola existens, extra circulum est et similiter ostendam quod sub puncto a deinceps, omnia puncta in peripheria parabolae, et tota penitus peripheria fertur extra circulum. Hoc idem ostendemus ex altera parte axis, et hoc est quod proponebatur demonstrandum.