XXIX. Hyperbolae, quarum non tangentes continent aequos angulos, sunt similes; et similium hyperbolarum non tangentes linea comprehendunt aequale angulos.

[S:191] Sunto duae hyperbolae ab, gd, quarum non tangentes ezh, tkl ipsos angulos ezh, tkl faciant aequales.

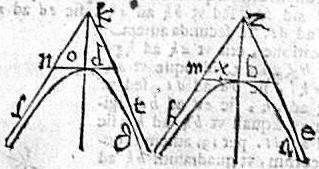
Aio quod similes sunt ipsae ab, gd hyperbolae. Sint enim ipsarum axes, atque eaedem semidiametri zb, kd, ad quas ordinate; et perinde ad rectos ducantur bm, dn, apud m, n puncta, coincidentes non tangentibus. Nam ipsae bm, dn, per 32. 1. conicorum, tangent sectiones; et per 3. 2, poterunt quadrantes specierum. Itaque ipsas zb, bm tertia proportionalis bx; et ipsas kd, dn tertia proportionalis subsequatur do. Eritque; per 16. 6. Euclidis, quadratum bm aequale rectangulo zbx. Itemque quadratum dn aequale rectangulo kdo. Igitur rectangulum zbx quadrans erit speciei in hyperbola ab; atque rectangulum kdo quadrans speciei in hyperbola gd; sed quadrans speciei comprehenditur sub semidiametri transversae. Igitur bx, do sunt semidiametri rectae. Ostendendum est itaque quod zh, kd sunt ipsis bx, do proportionales; et perinde diametri diametris proportionales; hoc modo anguli bzm, dkn sunt aequales: quandoquidem aequalium dimidii; anguli ad bd recti; et ob id similia sunt triangula zbm, kdn. Quamobrem sicut zb ad bm, sic kd ad dn, et perinde sicut quadratum zb ad quadratum bm, sic quadratum kd ad quadratum dn. Verum est (per 17. 6. Euclidis) zb ad bx; atque kd ad do. Ergo sicut zb ad bx, sic kd ad do, et ideo diametri diametris proportionales. Et propterea per 3. huius, ipsae ab, gd hyperbolae similes. Quod est primum ex propositis. Contra sint ab, gd hyperbolae similes. Aio iam quod et ipsi anguli ezh, tkl sunt aequales. Nam si similes sectiones, iam per conversam 3. huius, earum transversae rectis erunt proportionales; et perinde semidiametri semidiametris proportionales, hoc est sicut zb ad bx, sic iam kd ad do, et ideo per 17. 6. Euclidis, sicut quadratum zb ad quadratum bm, sic et quadratum kd ad quadratum dn, quare et sicut zb ad bm, sic kd ad dn. Igitur per 6. 6, aequiangula sunt ad invicem triangula zbm, kdn. Unde anguli bzm, dkn respondentes invicem aequales, et eorum dupli ezh, tkl invicem aequales erunt. Quod iam restabat demonstrandum.

Scholium

Quando autem ezh, tkl recti sunt tunc zb, bm aequales sunt, nec non kd, dn aequales, quare ipsaemet bm, dn sunt rectae diametri aequales iam transversis semidiametris. Ex qua aequalitate facilius arguitur sectionum similitudo, et ex similitudine aequalitas angulorum.

Scholium

Nec difficiulius ex 12. primi conicorum demonstrabimus, quod similes hyperbolae in duobus conis a planis erectis super triangulis per axes, recta basibus factae, aequidistant aequiangulis triangulis per vertices ductis. Et e contrario, quodque talia triangula, quibus aequidistant hyperbolae, angulos ad verticem coni habent aequales angulis, quos lineae non tangentes comprehendunt.