XXX. Si planum secet conum quemadmodum docet 13. primi conicorum, faciens ellipsim; atque in ipso triangulo per axim per extrema diametri transversae ipsius factae ellipsis ducantur sibi invicem coincidentes binae lineae, una quidem aequidistans basi trianguli; altera vero aequidistans lateri; tunc media proportionalis inter receptas ex aequidistante basi ab extremo diametri ad coincidentiam, et ad latus trianguli aequalis erit secundae diametro ellipsis. [S:192] Esto conus abg, cuius vertex b; basis ag; triangulum per axim abg facta ellipsis sicut docet 13. primi conicorum, sit cuius transversa in plano dicti trianguli de; item dz aequidistans ipsi ag, et eh aequidistans ipsi bg, ut in prima linearum est; aequidistans vero ipsi ab lateri, ut in secunda, et coincidens ipsi dz productae in 2, apud b. Demum linea dt sit media proportionalis inter ipsas bd, dz.

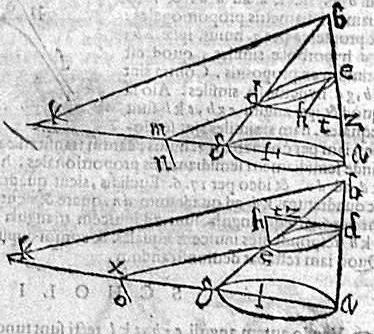
Dico iam quod dt linea est secundae diametro ipsius ellipsis de, quod sic ostenditur. Ducatur ipsi ed aequidistans bk, basique ag productae occurrens apud k; sitque inter ipsas gk, ka media proportionalis kl et propter aequidistantiam linearum erunt triangula abg, zeb similia item triangula gbk, hed similia in prima lineatione. In secunda vero triangula gbk, zed similia nec non triangula abk, zed similia in prima lineatione. In secunda vero triangula abk, hed similia. Quo sit ut respondentia latera sint proportionalia, itaque erit ut ak ad kg, sic zd ad dh. Et quoniam si dupla duplae ratio aequalis est, et simpla simplae aequalis erit. Ideo et ut ak ad kl, sic zd ad dt. Sed ut bk ad ak, sic ed ad zd. Igitur ex aequali ut bk ad kl, sic ed ad dt. In secunda autem lineatione, erit ut ak ad kg, sic hd ad dz. Ideoque ut ak ad kl, sic hd ad dt. Sed ut bk ad ak, sic ed ad hd. Igitur ex aequali ut bk ad kl sic ed ad dt, per 13. autem 1. conicorum, ut quadratum bk ad rectangulum akg; hoc est quadratum kl; sic diameter de ad rectam suam. Sed per 15.1 conicorum, secunda diameter media proportionalis est inter primam, suamque rectam. Ideoque, ratio diametri de ad rectam suam dupla est rationis de ad secundam diametrum, et ratio quadrati ad quadratum dupla est rationis lateris ad latus. Ergo ut bk ad kl, sic diameter de ad secundam diametrum, fuit autem ed ad dt, sicut bk ad kl. Igitur ut diameter de ad secundam suam, sic de ad dt, eamdem igitur rationem habet de ad secundam suam, et ad dt, quare per 9. quinti, dt aequalis est ipsi secundae diametro ellipsis de. Quod fuit demonstrandum.

Castello Bono Die 25. Octobris Hora 4. Noctis Indictione VI. 1547 Finis. LAUS DEO