[S:188] XXV. Si in quolibet cono triangulus per axem stet ad rectos basi: ellipses a planis super triangulum erectis, et auferentibus a vertice similia; verum sub contrarie posita triangula, similes sunt atque sub contrariae.

In cono abg, cuius vertex b, basis ag, triangulum abg per axem, sit ad rectos basi; duo autem plana ad rectos triangulo abg faciant duas ellipses, quarum diametri de, zh; hac lege ut triangulus bde similis sit triangulo bzh, atque sub contrariae positus, ut scilicet angulus bde sit aequalis angulo bzh, et reliquus reliquo.

Aio quod ellipses de, zh similes sunt. Nam cum ipsae de, zh non sint aequidistantes ipsi ag, coincident omnino ipsi ag, quare descedentes a vertice b; et ipsis de, zh aequidistantes, coincident ipsi ag productae; vel ad eamdem partem a vertice; vel ad diversas coincidant primum ad diversas, sintque bk ipsi de atque bl ipsi zh aequidistantes et quoniam angulus abl angulo bzh aequalis est, sibi coalterno; et angulus bgk aequalis angulo bde coalterno; et ipsi bde, bzh, per hyperbolen, sunt aequales. Idcirco aequales erunt anguli abl, gbk, quare per 18. huius, bk ad mediam proportionalem inter ak, kg; atque bl ad mediam proportionalem inter gl, la eamdem habebum, tam longitudine, quam potentia rationem. Igitur et ipsae ellipticae diametri de, zh (quae per 13. p, ad suas rectas ipsarum aequidistantium ad medias dictas, quo ad potentiam sequuntur rationes; ad coniugatas vero quo ad longitudinem) proportionales erunt tam rectis, quam coniugatis. Itaque per 4. huius ellipses de, zh similes sunt. Quod si de, zh, et earum aequidistantes coincidant ad eamdem partem a vertice b, concurrant versus partes bg: sic autem fiet ut a puncto g. Ipsis de, zh aequidistantes excitatae coincidant ipsi ab, coincidant. Sintque gk ipsi de, atque gl ipsi zh aequidistantes, mox ipsa gt secet anguli kgl per aequalia et quoniam angulus bgk aequalis est angulo bde; et angulus blg aequalis angulo bzh; et ipsi bde, bzh, per hyperbolen, sunt aequales.

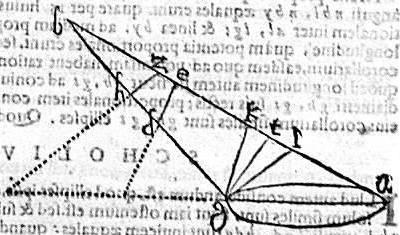
Idcirco aequales erunt anguli bgk, blg, et quoniam angulus btg aequalis est angulis blg, tlg intrinsecis. Angulis autem bgt aequalis angulis bgk, kgt. Iam aequales erunt anguli btg, bgt ex quibus demonstratis sequitur per praecedentem, ut ellipses, quarum diametri gk, gl similes sint. Sed per 6. huius, ellipsis gk similis est ellipsi de: quandoquidem sunt ab aequidistantibus planis, et eadem ratione similis est ellipsis zh, ellipsi gl; hoc est proportionales diametros habent ipsis per 6. huius. Sed per praemissam ellipses gk, gl proportionales diametros habent igitur et ipsae de, zh ellipses habent proportionales diametros: quandoquidem proportiones eidem aequales sunt inter se aequales. Quamobrem per 4. huius, ellipses de, zh similes sunt quod fuit demonstrandum. Appellantur autem cuiusmodi ellipses sub contrariae, quoniam a subcontrariis planis fiunt.