F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber sextus 20
<- App. -> <- = ->

XX. Si in cono scaleno triangulum per axem stet ad rectos basi; plana vero super triangulum erecta fecerint in cono sectiones quinque, quarum diametri aequidistent lineis descendentibus a vertice trianguli, ad partes lateris minoris ad basim extra productam, singulae singulis, hoc pacto, ut diameter primae sectionis aequidistet descendenti, quae cum cruribus trianguli extrinsecos angulos aequales facit: diameter secundae sectionis aequidistet descendenti, quae circulum triangulo, circumscriptum tangit; diameter tertiae sectionis aequidistet descendenti, quae periphaeriam sub vertice secat; diameter quartae sectionis aequidistet descendenti inter tangentem, et facientem aequos angulos cum cruribus trianguli; diameter demum quintae sectionis aequidistet extremae descendenti: tunc harum sectionum secunda circulus est; caeterae vero ellipses.

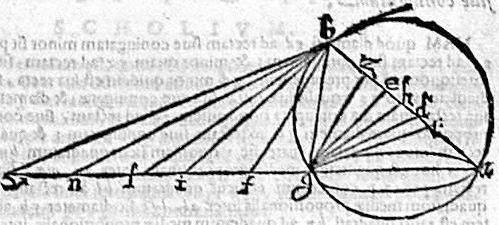
figura 19

Esto conus scalenus abg; cuius vertex b; basis ag; triangulum ad erectos basi abg; quinque autem plana recta ad triangulum abg, faciant totidem sectiones in cono; quarum diametri [S:186] aequidistent lineis descendentibus a vertice b, ad partes lateris minoris bg, basique ag eodem versus productae occurrant, hoc pacto; primam sectionem, cuius diameter gd aequidistet descendenti bn, quae angulos abx, gbn aequales facit; secundam cuius diameter ge aequidistet descendenti bi, quae tangit circulum abg apud b; tertiam cuius diameter gz aequidistet descendenti bf, quae periphaeriam bg secat apud k; quartam, cuius diameter gh aequidistet descendenti bl inter ipsas bi, bn; quintam, cuius diameter gt aequidistet ipsi bi extremae descendentium. Dico iam quod sectio, cuius diameter ge circulus est. Nam cum per 29.3. Euclidis, angulus gbi, et perinde ipsius coalternus bge sit aequalis angulo bag. Iam planum faciens sectionem, cuius diameter ge, aufert triangulum gbe simile, ac sub contrarium triangulo abg, quare per 5. primi conicorum, sectio, cuius diameter ge circulus est. Reliquae autem sectiones, quarum diametri gd, gz, gh, gt nec aequidistantes ipsi ag; nec sub contrariae sunt, per 13. eiusdem, ellipses. Quemadmodum proponitur demonstrandum.

Inizio della pagina
 ->