XIX. Si in quolibet cono triangulus per axim fiet ad rectos basiplana vero super triangulum erecta fecerint ellipses, quarum transversae diametri aequidistent descendentibus lineis a vertice trianguli, et infra secantibus periphaeriam circuli triangulum circumscribentis, basique productae coincidentibus; diameter ellipseos aequidistans descendenti quae prius occurrit basi productae maiorem rationem habet ad suam rectam diametrum, et ad suam coniugatam.

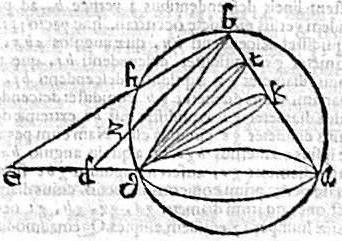
In cono, cuius vertex b; basis ag; triangulus per axem ad rectos basi abg; plana duo ad rectos triangulo abg, faciant duas ellipses. Unam, cuius diameter gt aequidistet lineae bzd, secanti apud z periphaeriam circuli abg, et occurrenti apud d punctum basi ag, productae, et alteram, cuius diameter gh aequidistet lineae bhe, quae secat periphaeriam apud h, et excipitur a basi apud e. Dico itaque quod gt diameter aequidistans descendenti bd, quae prius excipitur a basi producta maiorem rationem habet ad suam rectam diametrum, quam diameter gk ad suam rectam. Namque per 17. huius, lineae bd proportio maior est ad lineam mediam proportionalem inter ad, dg; quam lineae be ad mediam proportionalem inter ae, eg, maior inquam proportio tam longitudine, quam potentia. Sed per 13 p. conicorum, sicut est quadratum bd ad rectangulum adg; hoc est, ad quadratum mediae inter ad, dg: sic [S:185] diameter gt ad rectam diametrum, et sicut quadratum be ad rectangulum aeg; hoc est ad quadratum mediae inter ae, eg; sic gk ad rectam suam.

Item per corollarium 13. dictae, sicut bd ad mediam proportionalem inter ad, dg; sic diameter gt ad suam coniugatam. Et sicut be ad mediam proportionalem inter ae, eg, sic gk ad suam coniugatam. Igitur maior est proportio diametri gt ad suam coniugatam; quam diametri gk ad suam coniugatam. Quemadmodum, proponitur demonstrandum.

Manifestum est ergo quod in huiusmodi ellipsibus transversae, diametri sunt maiores suis rectis, suisque coniugatis diametris: quandoquidem descendentes, quibus aequidistant transversae medis proportionalibus, dicto modo sumptis, et longitudine, et potentia sunt maiores. Quod quidem in cono recto semper accidit.

Item ellipsium eo modo factarum, illa, cuius transversa diameter acutius triangulum aufert a vertice, longior est: hoc est ellipsis, cuius diameter gt longior est, quam ellipsis, cuius diameter gk: quandoquidem gt, diameter ad suam coniugatam maior est proportio, quam dk diameter ad suam coniugatam; et perinde longioris est formae.