XVI. A vertice dati trianguli ad partes cruris reliquo minoris ad basim extra productam deducere lineam, quae datam habeat rationem ad mediam proportionalem inter adiectam basi, et eam, quae ex basi, et adiecta constat. Oportet autem datam rationem non minorem esse ea, quam habet linea ab ipso vertice deducta aequales angulos extrinsecos cum cruribus trianguli faciens, basique productae coincidens ad mediam proportionalem dicto modo sumptam.

Sit datum triangulum abg; data ratio, quae ed ad dz. Oportet a vertice b ad partes lateris bg; ipso latere ab minorem, lineam deducere, quemadmodum proponitur. Perficietur problema repetita iam descriptione praecedentis. Itaque si data ratio fuerit aequalitatis, tunc per punctum b ductaur linea ubi, tangens in b puncto circulum bgp; atque conincidens basi ag productae apud i punctum. Nam tunc linea bi erit quam petimus. Cum quadratum bi, per 35. 3. aequum sit rectangulo aig; et perinde per 16. 6. sit media proportionalis inter ai, ig. Si autem data ratio sit maioris ad minus; tunc per corollarium praecedentis, linea ducenda secabit periphaeria bg, [S:182] quare tunc linea ducenda ducetur omnino per 13. 1. huius.

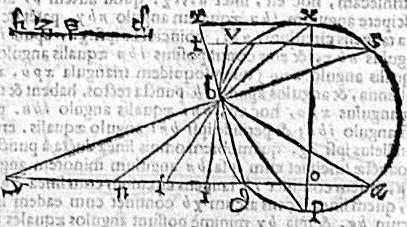
Demum si data ratio sit minoris ad maius: linea quaesita secabit periphaeriam supra b punctum, et necessarium erit rationem datam tunc non minorem esse ea, quam habet linea bn, faciens angulos xba, pbn aequales ad mediam proportionalem inter an, ng: secus enim problema esset impossibile, per praecedentem, quandoquidem, ratio bn ad mediam dictam minima est omnium descendentium ad suas medias. Sit ergo tunc data ratio, quae ed ad dz et si fuerit ed ad dz, sicut bn ad mediam proportionalem inter an, ng. Iam ipsa bn erit linea, quam ductum iri volumus. Si autem proportio ed ad dz maior fuerit quam bn ad mediam dictam. Tunc sit per 9. 6. Euclidis, sicut ed ad dz, sic dz ad dh; ut scilicet ipsae ed, dz, dh sint continue proportionales, cumque; media proportionalis inter an, ng sit et media proportionalis inter bn, nx, per 35. 3 et 16. 6. Euclidis. Iam pridem proportio ed ad dh maior erit, quam bn ad nx: quandoquidem simpla simplam superante, et dupla ratio duplam excedet. Sed propter similitudinem triangulorum bgn, brx, sicut bn ad nx, sic iam bg ad gr. Igitur est maior ratio ed ad dh, quam bg ad gr; et disiunctim maior est ratio ed ad eh, quam gb ad br. Sit itaque sicut de ad eh, sic bg ad bt. Eritque per 10. 5. Euclidis, linea bt minor quam br, quare linea per t punctum aequidistans ipsis xr, ag secabit omnino periphaeriam circuli duobus in locis, secet in punctis k, s; et coniuncta k, b, et producta coincidat basi ag, protense apud l. Item coniuncta sb, et producta coincidat basi dictae apud y. Dico igitur tam lineam bl, quam by esse illam, quam ductum iri volumus. Nam propter similitudinem triangulorum bgl, btk, est sicut gb ad bt; et perinde sicut de ad eh, sic lb, ad bk; et conversim sicut he, ad ed, sic kb ad bl; et coniunctim sicut hd ad de, sic kl ad lb; et rursus conversim sicut ed ad dh, sic bl ad lk; quare, et sic by ad ys. Igitur et sicut ed ad dz, sic bl ad mediam proportionalem inter bl, lk: hoc est mediam proportionalem inter al, lg. Itemque et sic by ad mediam proportionalem inter by, ys: hoc est mediam proportionalem inter ay, yg: quandoquidem si dupla ratio aequalis est duplae, et simpla aequalis est simplae. Itaque tam bl linea, quam by est quae a vertice b ad basim ag productam ducenda proponitur.