XIV. A vertice trianguli ad partes cruris reliquo minoris linea ducta, basique extra productae coincidens:tunc minimam habet rationem ad mediam proportionalem inter adiectam basi, et eam, quae ex basi, et adiecta constat, quando aequales facit cum cruribus trianguli extrinsecos angulos.

Sit triangulum abg, a cuius vertice b ad partes lateris bg ipso ab minoris ducatur liea xbn, coincidens ipsi ag basi productae apud punctum n; hac scilicet conditione, ut anguli extrinseci xba, gbn sint aequales. Dico iam quod linea bn minimam habet rationem ad mediam proportionalem inter gn, na omnium rationum quas habent ab eodem b vertice ductae lineae, eidemque basi productae coincidentes, ad medias similiter sumptas proportionales. Circumscribatur enim per 5. 4. Euclidis, triangulo abg circulus bgp; sectoque per medium angulo abg, ducta bp ad periphaeriam, erunt anguli xbp, pbn aequales quandoquidem singuli ex binis constant aequalibus; et ideo recti per diffinitionem. Rectus ergo cum sit angulus pbx, et linea bp subrendat arcum pgb, minorem semicirculo. Iam bx complebit semicirculum, per 20. 3. Euclidis; et ideo coniuncta px dyameter erit; quae cum secet arcum apg per aequalia: secabit, et chordam ag, ut puta in puncto o per medium, et ad rectos. quare xb ad rectos ipsi px dyametro, per 15. 3. circulum tangens, aequidistabit ipsi ag. Coincidat itaque gb producta ipsi xr apud r, et a vertice b deducatur alia, quaevis linea coincidens ipsi ag productae, ut pote bl. Iam demonstrandum est quod bn minorem habet rationem ad mediam proportionalem inter an, ng; quam linea, bl ad mediam proportionalem inter ab, lg. Ponatur enim ducta inter ipsas gb, bn, et tunc aut secabit arcum bx, aut tanget circulum apud b, aut secabit arcum bg. Si secabit arcum bx, secet apud k; et ducatur kt aequidistans ipsis xr, ag; et coincidens ipsi br, apud t punctum, et erit minor proportio bg ad gr, quam bg ad gt. Sed propter aequidistantiam linearum, et similitudinem triangulorum; sicut bg ad gr, sic bn ad nx, quam bl ad mediam proportionalem inter bl, lk. (quandoquidem si dupla proportio minor est quam dupla; et simpla minor est quam simpla) [S:180] verum media proportionalis inter bn, nx, per 35. 3, est etiam media proportionalis inter an, ng, et media proportionalis inter bl, lk, est et media proportionalis inter al, lg.

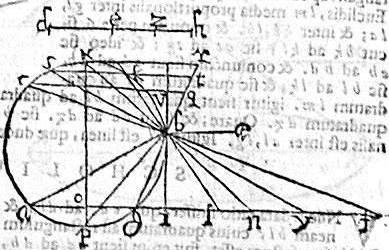
Ergo minor erit ratio bn ad mediam proportionalem inter an, ng, quam bl ad mediam proportionalem inter al, lg. Quod est propositum. Quod si bl tangeret circulum apud b, tunc per 35. 3, ipsamet bl esset media proportionalis inter al, lg. Cumque bn sit minor media proportionali inter bn, nx; hoc est media proportionali inter an, ng, rursus patet propositum. Demum si bi secaret arcum bg; tunc maior esset quam media proportionalis inter ipsam, et partem sui extrinsecam circulo; unde a fortiori magis constaret propositum. Nunc autem sumatur linea ducta a vertice b coincidensque ipsi ag productae ultra punctum n, ut pote by, quae producta secet circulum apud s; et producta st penes ipsas xr, ag. Non aliter quam in primo casu demonstrabimus minorem esse rationem bn ad nx, quam by ad ys: et perinde minorem esse proportionem bn ad mediam proportionalem inter bn, nx, hoc est, mediam proportionalem inter an, ng, quam by ad mediam proportionalem inter by, ys; hoc est mediam proportionalem inter ay, yg. Quod est propositum. Item ductaur linea bf, coincidens ipsi ag producta ultra punctum y, iam similiter ea producta donec occurrat peripheriae apud punctum c; atque ipsa cq penes ipsas xr, ag. Ostendemus quod minor est ratio by, ad mediam proportionalem inter ay, yg, quam bf ad mediam proportionalem inter af, fg. Et similiter id ipsum ostendemus de linea bl collata ad quamvis lineam descedentem a puncto b ad aliquod punctum inter l, g in ipsa lg linea. Ostensum est ergo quod ratio bn minor est ad mediam proportionalem inter an, ng; quam bl ad mediam proportionalem inter al, lg; et quam by ad mediam proportionalem inter ay, yg; quodque by ad mediam proportionalem inter ay, yg, est proportio minor quam bf ad mediam proportionalem inter af, fg, et similiter bl collata ad quamvis descendentem inter ipsas bg, bl. Itaque bn inter omnes a vertice b ad basim dg productam descendentes, ipsa bn minimam habet rationem ad mediam proportionalem, tali modo sumpram. Quod iam demonstrandum proponitur.