XXIX. Quod si quinque memoratae sectiones ad eumdem axem adiacentes, ac sub eodem vertice, sese vicissim super uno puncto secent; iam tunc ipsarum ordo praeposterus erit ad praedictum: nam earum intima erit hyperbolae; quae quidem cadet intra parabolen; quae intra ellipsim axis longioris; quae intra circulum; qui tandem intra ellipsim axis, brevioris omnium extremam, ad ipsum tamen ut antea verticem sese tangentes.

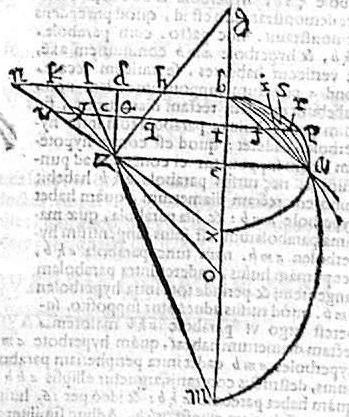
Sit ellipsis apb, cuius axis bx; circulus arb, cuius diameter bo; ellipsis asb, cuius axis longior bm; parabole aib, cuius recta diameter bd; hyperbole afb, cuius transversa bg. Demonstrandum est quod hyperbole afb cadit intra parabolen aib; parabole autem intra ellipsim asb, axis longioris ; ellipsim autem asb intra circulum arb. Circulus denique intra ellipsim apb, axis brevioris. Dum scilicet omnes hae quinque sectiones secant se invicem apud unum a punctum. Ducatur enim a puncto a ordinate ad axim linea ae, et producatur, ponaturque ipsi oe aequalis ez; et coniungatur gz, secans bd apud b. Item coniungantur mz, oz, xz, et producantur donec ipsi bd productae occurrant apud puncta l, k, m. Et cum in circulo linea ae possit rectangulum beo, quod est rectangulum bez. Et per 11.p, in parabola aib, possit linea ae rectangulum dbe. Iam aequale erit ez ipsi bd, quare dbez parallelogrammum rectangulum erit quod potest ae ordinate ducta in una quaque sectionum. Igitur rectangulum dbez, adiacens ad be receptam ab ipsa ae, ordinate ducta. Ita filtitur, ut angulus z sit in linea quae coniungit extremum transversae, cum extremo rectae diametri. Sed extremum transversae in hyperbola est g punctum, in ellipsi asb est m punctum in circulo o punctum in ellipsi apb est x punctum. Igitur recta diameter hyperboles afb erit bh; ellipsis asb erit bl; circuli erit bk; ellipsis dpb erit bn. Itaque per punctum t utcumque relictum in linea be ducatur ordinate linea, coincidens sectionibus apud p, r, s, i, f, puncta; ipsisque zb, zd, zl, zk, zn apud puncta q, , s, y, u. Et tunc in hyperbola quidem linea ft poterit [S:169] rectangulum btq; in parabola vero linea ib poterit rectangulum bt, maius quare brevior erit ft, quam ti; et f punctum in peripheria hyperboles erit intra parabolen aib.

Et similiter omne aliud punctum in peripheria hyperboles, et ipsa peripheria tota afg erit intra parabolam. Non aliter quoniam st in ellipsi asb potest rectangulum btc, maius rectangulo bt, quod potest linea ti. Arguetur linea ti brevior quam linea ts; et peripheria paraboles aib intra ellipsim asb. Item quoniam in circulo linea rt potest rectangulum bty, maius rectangulum btc, quod potest linea st. Arguetur linea st brevior, quam linea rs, et peripheria ellipsis asb intra circulum arb. Denique quoniam in ellipsi apb linea ps potest rectangulum btu, maius rectangulo bty, quod poterit linea rt, constabit linea rt brevior, quam linea pt; et peripheria circuli arb, intra ellipsim apb contineri. Et solum b verticis punctum peripheriis sectionum ipsarum esse commune. Quae fuerant demonstranda.

SCHOLIUM

Notandum quod harum quinque sectionum peripheriae super a punctum se vicissim secantes, sub ipso deinceps puncto in contraria feruntur inverso ordine, ut hyperbole; quae intima erat fiat iam extrema; atque ellipsis quae fuerat extra. Iam inde intima feratur; fient et ipsae rectae lineae diametrorum extrema coniungentes atque in ipso z puncto se vicissim secantes sub tali protinus puncto in contraria feruntur.