XXX. Eisdem utique suppositis: id, quod duae praemissae proponunt brevissime demonstrare.

Sint circa eumdem axim, ac sub eodem vertice quinque praedictae sectiones, videlicet hyperbole ab; parabole be; ellipsis bzg, ad axem longiorem bg; circulus bht, cuius diameter bt; ellipsis bkl, ad axem breviorem bl, quarum sectionum communis recta diameter; sit bd.

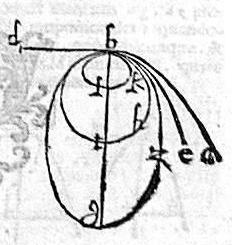
Demonstrandum est paucis id, quod 28, praecedens demonstravit. Hoc pacto. Cum circulus bht, ad axem breviorem, verticemque; ellipsis bkl positus, diametrum bt aequalem ipsi bd, qua recta diametros ellipsis bkl est, habeat. Iam per 12. huius, ellipsis bkl intra circulum bht cadet. Similiter per 9. huius, circulus bht intra ellipsim bzg. Atque, ellipsis bzg, per 15. huius, intra parabola eb. Nec non parabola eb, per 21. huius, intra hyperbolen ab feretur omnes, per easdem apud ipsum b verticem se invicem tangentes. Quod est propositum. Rursus ponantur circa unum axem, unumque verticem, quinque memoratae sectiones; [S:170] ita ut super unum punctum a se invicem secent, sicut 29. praemissa suppofuit: videlicet, ellipsis agb, ad axem breviorem bd, circulus aeb, cuius diameter bz; ellipsis ahb, ad axem longiorem bt; parabole kab; hyperbole mab.

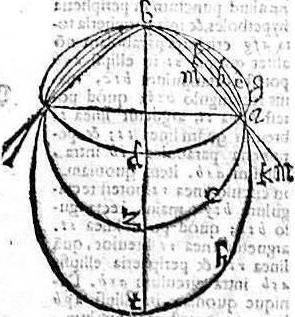
Iam breviter demonstrandum est id, quod praecedens demonstravit. Hoc pacto. Cum parabole akb, et hyperbole amb communem axem, ac verticem habentes, se invicem secare apud a punctum supponantur. Iam non habebunt eamdem rectam diametrum; sic enim per 21. huius, parabola tota intra hyperbolen caderet. Quod est contra hypotesim, cum supponatur ei coincidere ad punctum a. Nec rursus parabole akb habebit minorem rectam diametrum, quam habet hyperbole amb; et illa parabola, quae maxima parabolarum est intus tangentium hyperbolen amb. Nam tunc parabola akb, per primam huius, caderet intra parabolam tangentem; et perinde tota intra hyperbolen amb. Quod rursus adversatur supposito. Superset ergo ut parabole akb maiorem rectam diametrum habeat, quam hyperbole amb, quare per 21. huius, peripheria hyperboles amb cadet intra peripheriam parabolae akb. Similiter per 15. et primam huius, destructis contrariis, arguetur ellipsis ahb habere maiorem rectam diametrum, quam habet parabole akb; et ideo per 16. huius, peripheria paraboles akb cadet intra peripheriam ellipsis abh. Adhuc similiter argumentaado per 9. et 1. huius, confutatis contrariis, arguetur circulus aeb habere maiorem rectam diametrum, quam habet ellipsis ahb, et ideo per 10. huius, peripheria ellipsis ahb caderet intra peripheriam circuli aeb. Demum non aliter per 12. et 1. huius, indirecte ostendetur ellipsis agb habere maiorem rectam diametrum diametro circuli aeb; et propterea per 13. huius, peripheria circularis aeb ferri intra ellipsim agb. Omnes tamen apud b se invicem contingerent. Et haec fuerant demonstranda.

FINIS LIBRI QUINTI