XXVI. Si super eumdem axim, ac sub eodem vertice constituantur quinque sectiones eamdem rectam diametrum habentes: earum intima erit ellipsis ad axem minorem adiacens; quae quidem cadet intra circulum, qui intra ellipsim ad axem maiorem constitutam; quae intra parabolam; quae eamdem intra hyperbolem omnium extremam ad ipsum verticem sese tangentes.

Sit hyperbole ab, parabola kb, ellipsis lb, adiacens ad axem maiorem bl, circulus mb; ellipsis nb, adiacens ad axem minorem bz, transversa hyperboles bg; recta diameter his quinque sectionibus communis bd; circuli diameter be ipsi bd aequalis. Demonstrandum est quod ellipsis nb cadit intra circulum bm; circulus autem intra ellipsim bl; ellipsis autem bl intra parabolen kb; parabole demum intra hyperbolen ab; quodque omnes sese contingunt apud b verticem. Hoc pacto, coniungatur gd, et producatur; coniungatur item z, e, b puncta cum d puncto, productis lineis zd, ed, hd. Deinde per quodvis relictum punctum in axe be, ut pote t ordinate ducatur linea, coincidens singularum sectionum peripheriis apud a, k, l, m, n puncta, ipsisque, zd, ed, bd, ipsisque gd producta, apud x, o, p, s puncta; [S:168] ipsa autem dr perpendicularis descendat ad ordinatam.

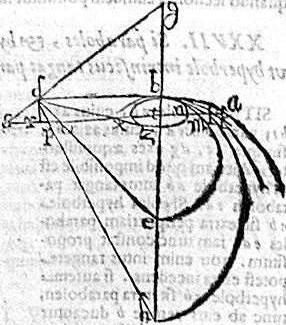
Sic tr aequalis erit ipsi bd, quibus punctis. Iam per 13. vel 15.primi Conicorum, nt poterit rectangulum btx, at mt poterit rectangulum bte, hoc est rectangulum bto, maius ipso rectangulo btx. Igitur brevior nt, quam tm: et perinde punctum m, et similiter quodvis aliud punctum in peripheria ellipsis bn; et ideo tota peripheria cadet intra circulum mb. Non aliter quoniam mt potest rectangulum bto, at lt potest rectangulum btp; per 13.primi Conicorum, maius ipso rectangulo bto; arguetur mt brevior, quam tl. Et perinde peripheria circuli bm intra peripheriam ellipsis lb. Item quoniam kt, per 11.primi Conicorum, potest rectangulum btr, maius ipso rectangulo btp. Arguetur tl brevior quam tk; et ideo peripheria ellipsis lb intra peripheriam parabolae kb. Denique quoniam at, 12.primi Conicorum, potest rectangulum bts, maius ipso rectangulo btr, constabit ks brevior quam ta. Et propterea peripheria paraboles kb intra peripheriam hyperboles ab contineri ostendetur, solum autem punctum b, quod extremum est axium, et vertex sectionibus communis communicatur a cunctis peripheriis, in quo sese vicissim contingunt. Haec erant, quae proponebantur demonstranda.