XXI. Parabole habens eamdem rectam diametrum cum hyperbola, eumdem axim, atque verticem: intus eam tangens apud verticem, tota intra eam cadit.

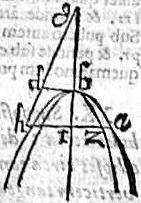
Sit hyperbole ab, cuius transversa bg; recta vero diameter bd, parabole autem circa eumdem axim sit bz, habens eamdem rectam bd. Aio iam quod parabola bz tangens hyperbolen ab, apud b verticem, tota intra hyperbolen ab cadit. Capiatur enim in peripheria paraboles utcumque relictum punctum z, per quod ordinate ducatur azth; coincidens hyperbolae, axi, et ipsi gd coniunctae, atque productae, apud puncta a, z, h, itaque per 11.primi Conicorum, linea zt poterit rectangulum dbt, in parabola; etper 12. eiusdem, at poterit rectangulum bth, in hyperbola, maius quidem ipso rectangulo dbt, quare brevior erit zt, quam at. Itaque punctum z; et similiter omne aliud punctum in peripheria paraboles; et perinde tota eius peripheria, cadet intra hyperbolen ab. Idemque fiet ad reliquas partes axis. Quemadmodum proponitur demonstrandum.