[S:165] XXII. Eisdem subiectis. Si paraboles recta ponatur maior quam recta hyperboles: tunc parabole extra procedens utrinque coincidet hyperbole.
Eisdem manentibus.
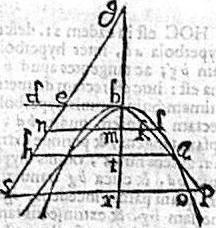
Sit paraboles alb recta bd, maior quam be recta hyperboles akb. Aio tunc quod alb parabole partim extra hyperbolen akb circumlata coincidit eidem. Agatur enim a puncto d axi bt aequidistans, ipsique ge coniunctae, ac productae concurrens apud b, linea db; et per b punctum ordinate ducatur in hyperbola linea bta. Et tunc per 12.primi Conicorum, in hyperbola linea at poterit rectangulum bth; at per 11. eiusdem, in parabola ordinate ducta a puncto t poterit rectangulum dbt; quod aequale est rectangulo bth, quare talis ordinate ducta in parabola erit ipsamet at linea. Et perinde a punctum est in utraque peripheria, unde necesse est hyperboles, et paraboles peripherias super eodem puncto a se invicem secare. Nam si capiatur relictum punctum k in peripheria hyperboles inter a, b puncta; et per ipsum ordinate ducatur lkmn, coincidens parabolae, axi, et ipsi ge productae apud l, m, n puncta. Iam per 12.p.Conicorum, km poterit rectangulum bmn in hyperbola; at in parabola per 11. eiusdem, lm poterit rectangulum dbm, maius ipso rectangulo bmn. Quamobrem lm longior quam mk; et ideo punctum l; et omne aliud punctum in peripheria paraboles, inter a, b puncta, et tota talis peripheria cadet extra hyperbolen. Sub puncto autem a per relictum punctum o in parabola ducatur ordinate linea pors. Coincidens hyperbolae, axi, et ipsi ge productae apud p, r, s puncta. Et tunc 11. vero eiusdem, in parabola, linea or poterit rectangulum dbr, minus quidem rectangulo brs, propterea or brevior erit, quam rp; et punctum a, et omne aliud punctum sub puncto a in peripheria paraboles; et tota ipsa deinceps peripheria cadet intra hyperbolen. Id idem ad reliquas axis partes ostendemus. Sicut proponitur demonstrandum.