VII.

Eisdem sup⁹⁵positis, si circuli diameter ponatur maior quam⁹⁶ recta hyperboles, tunc circulus sectionem in vertice tangens, extraque partim incedens, rursus hinc et inde secando ipsi coincidet⁹⁷.

Iisdem manentibus, ponatur be circuli⁹⁸ diameter maior quam bd recta hyperboles. Aio tunc quod abe⁹⁹ circulus tanget¹⁰⁰ hyperbolen in puncto b, et inde extra¹⁰¹ incedens hinc et inde, rursus¹⁰² hyperbolae secando coincidet. Nam, cum be maior sit quam [S:156] bd, producatur bd ponaturque ipsi be aequalis bz, et coniugatur gd, et producta coincidat ipsi ez coniunctae apud h punctum, per quod ordinate ducatur hta, coincidens axi apud t atque hyperbolae apud a.

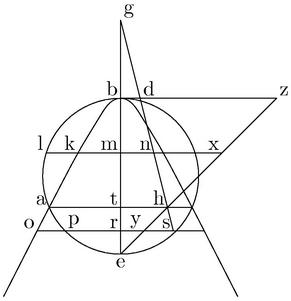
Et iam ostendam quod circulus in ipsomet A¹⁰³ puncto secat hyperbolen. Namque, per 12. I. Conicorum, in hyperbola ordinata at¹⁰⁴ potest rectangulum bth. Atque in circulo ordinate ducta a¹⁰⁵ puncto t potest rectangulum bte, quod est ipsum rectangulum bth, quandoquidem aequales sunt th, te¹⁰⁶. Igitur ordinate¹⁰⁷ ducta in circulo est ipsa ta. Et perinde punctum a commune est utrique peripheriae. Unde necesse est eas se invicem super a puncto secare. Arcus autem circuli bla incedit extra hyperbolen. Capiatur enim in peripheria Hyperboles¹⁰⁸ punctum quodvis relictum inter a, b puncta, quod sit k. Per quod ordinate ducatur¹⁰⁹ lkmnx, coincidens circulo, axi, ipsisque gh, ez lineis, apud l, m, n, x puncta. Et tunc per 12. I. Conicorum, km quidem poterit rectangulum bmn. Et¹¹⁰ in circulo lm poterit rectangulum bme, quod est rectangulum bmx, maius ipso rectangulo bmn. Itaque brevior erit km quam lm. Et idcirco punctum l, quod in peripheria circuli iacet¹¹¹, extra hyperbolen est. Similiter omnia puncta in arcu circuli bla, atque adeo totus arcus bla cadit extra hyperbolen. Sub puncto¹¹² autem a peripheria¹¹³ hyperboles cadit deinceps semper extra circulum. Quod enim de¹¹⁴ puncto¹¹⁵, idem de omnibus, et tota peripheria demonstrabitur: ut si per punctum o in peripheria hyperboles infra punctum a utcunque relictum, ducatur ordinate o¹¹⁶prys, coincidens circulo, axi, ipsi ez, ipsique gh productae, apud puncta p, r, y, s. Iam per 12. primi Conicorum, or linea¹¹⁷ poterit rectangulum brs. Verum in circulo pr poterit rectangulum¹¹⁸ bre, quod est rectangulum bry, minus quidem ipso rectangulo brs, quare longior or quam pr. Et ideo o punctum extra circulum. Haec eadem ostendemus in peripheriis ad reliquas partes axis. Sicut¹¹⁹ proponitur demonstrandum.