X.
Eisdem suppositis, si circuli diameter ponatur maior quam recta ellipsis, minor tamen axe, tunc circulus partim extra sectionem cadens, intra153 eam154 utrinque secando revertitur.
Iisdem manentibus, ponatur circuli diametros be, maior quam recta ellipsis bd. Aio tunc quod circulus bae, tangens quidem apud b ellipsim, mox egressus, sectio[S:158]nem secabit eam hinc et inde. Nam, cum be sit maior quam bd, producatur bd ponaturque ipsi be aequalis bz atque ipsae gd, ez coniunctae secent se vicissim155 apud h punctum, per quod ordinate agatur linea hta, coincidens axi quidem apud t, ellipsi vero apud a punctum. Unde per 13. 1. Conicorum in ellipsi applicata156 at poterit rectangulum bth. Cumque in circulo ordinate ducta ad punctum t possit rectangulum bte, quod est ipsum rectangulum bth, iam pridem157, ordinate ducta in circulo erit ipsamet ta, et perinde a punctum erit tam in peripheria ellipsis, quam in peripheria circuli.
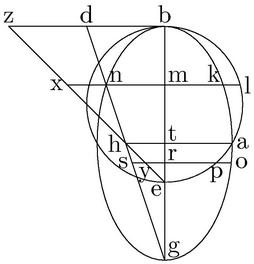
Secant itaque se peripheriae super a punctum. Arcus autem158 bla circuli cadet extra sectionem. Capiatur enim in peripheria ellipsis inter159 puncta a, b quodvis relictum punctum k, per quod ordinate agatur lkmnx, coincidens circulo, axi, ipsique dg, ez, apud l, m, n, x160 puncta. Et tunc per 13.[C:6v] 1. Conicorum, in ellipsi linea km poterit rectangulum bmn, in circulo autem lm poterit rectangulum bme, quod est rectangulum bmx, maius quidem ipso rectangulo161 bmn. Itaque longior erit lm quam km. Et perinde punctum l in peripheria circuli, et similiter omnia eius puncta, et totus arcus bla, erit extra ellipsim. Sub puncto autem a deinceps circulus intra sectionem cadet. Ducta enim per punctum o in ellipsi utcunque relictum, linea oprys ordinate, coincidens circulo, axi, ipsisque gd, ez apud ipsa p, r, s, y162 iam163. per 13. 1.164 in ellipsi, or poterit rectangulum brs. In circulo autem pr poterit rectangulm bre, hoc est rectangulum bry, quod ipso rectangulo brs165 minus est. Et ideo pr brevior quam or166. Unde punctum p intra ellipsim. Et similiter omnia puncta peripheriae circuli sub puncto a, et ipsa peripheria tota, intra sectionem cadet. Quae omnia de peripheriis ellipsis, et circuli ad reliquas partes axis167 ostendam. Quemadmodum proponebatur demonstrandum.