IX.

Circulus ad verticem maioris axium ellipsis, super ipsum axim¹⁴⁵ constitutus, habens diametrum aequalem rectae diametro sectionis, in vertice tangit sectionem totus intra ipsam cadens.

Sit ellipsis ab, cuius maior axium bg¹⁴⁶, recta diameter bd, cui aequalis ex axe capiatur be, superque¹⁴⁷ circulus describatur bze.

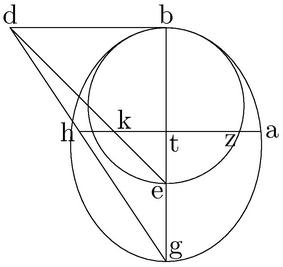
Aio quod circulus bze ellipsim apud b verticem tangens, totus intra sectionem cadit. Capiatur, enim, in periphaeria [C:6r] circuli quodlibet relictum punctum z, et ordinate¹⁴⁸ agatur aztk¹⁴⁹h, coincidens ellipsis, axi¹⁵⁰, ipsisque ed, dg, coniunctis apud ipse¹⁵¹ a, t, k, h puncta. Unde cum per 13. 1. Conicorum, at possit rectangulum bth, atque in circulo zt possit rectangulum bte, quod est rectangulum btk, minus ipso rectangulo bth. Iam brevior erit zt quam at. Et perinde ipsum z punctum cadit intra sectionem. Et similiter ostendam quod omnia puncta in peripheria bze¹⁵² circuli, et ideo tota omnino peripheria circuli, cadet intra sectionem, in solo b puncto ipsam tangens. Et hoc est quod proponebatur a principio demonstrandum.