F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 56
<- App. -| <- = -|

[A:97r] 56a Si alteram contrapositarum duae lineae tangentes coincidant: per tactus autem aequidistantes ducantur tangentibus: et a tactibus per idem punctum alterius periferiae ducantur lineae, quae secent aequidistantes; contentum tetragonum sub abscissis rationem habebit ad quadratum iungentis tactus compositam ex ea, quam habet connectens concursum tangentium cum puncto medio iungentis tactus, quae est inter punctum medium et alteram periferiam, ad eam, quae est inter eadem periferiam et concursum potentia: et ex ea, quam habet contentum sub tangentibus ad quadratum, quod fit ex dimidia iungentis tactus.

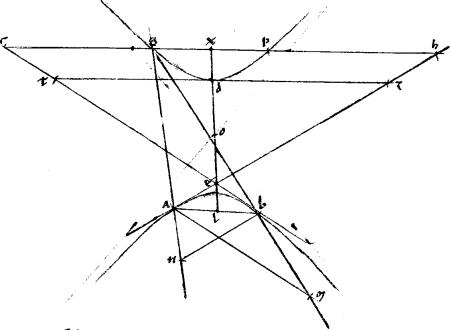figura 1
1 Sint contrapositae ab gd. // Quarum centrum o. // Tangentes aezh betc. // Coniungens tactus ab. // Quae per medium secetur apud l. // Et coniuncta le producatur per puncta odx diameter enim erit, per 29am secundi Conicorum. // Ipsi autem ae aequidistans linea bn. // Ipsique be aequidistans linea am. // Et per relictum in altera sectionum punctum g perque tactus a b [A:97v] agantur lineae gan gbm.
2 // Dico iam quod ratio rettangolo bn am ad quadrato ab1 componitur ex rationibus
angolare aperta quadrato ld ad quadrato de
rettangolo aeb ad quadrato al
.
// Ducantur enim per puncta g d aequidistantes ipsi ab lineae cgxph tdz. // Eruntque, propter similitudinem triangulorum quoniam al lb sunt aequales: et ipsae td dz aequales: itemque cx xh aequales2. 3 // Cumque gp sit ordinata, et perinde gx xp aequales supererunt et cg ph aequales. // Et, quoniam, per 18am huius tertii, ut quadrato bt ad quadrato3 tdz sic quadrato bc ad rettangolo pcg hoc est ad rettangolo cgh. // Estque, propter proportionem linearum ut ad rettangolo za tb ad quadrato tb sic ad rettangolo ha cb ad quadrato bc. // Idcirco, ex aequali, erit ut ad rettangolo za tb ad quadrato4 tdz sic ad rettangolo ha cb ad rettangolo cgh.
4 // Assumpto autem medio rettangolo tez ratio rettangolo za tb ad rettangolo tdz5 componitur ex rationibus
angolare aperta rettangolo za tb ad rettangolo tez
rettangolo tez ad rettangolo tdz
//.
Estque, propter similiter sectas, ut ad rettangolo za tb ad rettangolo tez sic quadrato ld ad quadrato de. // Utque ad rettangolo tez ad quadrato6 tdz sic ad rettangolo aeb ad rettangolo alb. //
5 Igitur et ratio rettangolo ha bc ad rettangolo cgh componetur ex rationibus
angolare aperta quadrato ld ad quadrato de
quadrato aeb ad rettangolo alb
.
6 // Habetque, per 24am sexti Euclidis ratio rettangolo ha bc ad rettangolo cgh rationem compositam
ex rationibus
angolare aperta bc ad cg
ah ad hg
.
// Et propter similitudinem triangulorum ut bc ad cg sic ma ad ab. // Utque ah ad hg sic nb ad ba. // Verum, per 24am sexti ratio rettangolo am bn ad quadrato ab componitur
ex rationibus
angolare aperta ma ad ab
nb ad ba
hoc est ex rationibus
angolare aperta bc ad cg
ah ad hg
et ideo [S:128] ex rationibus
angolare aperta quadrato ld ad quadrato de
rettangolo aeb ad quadrato alb
.
// Quod iam proponebatur demonstrandum.

[A:98r]

TERTII LIBRI CONICORUM APOLLONII

PERGAEI FINIS

Panhormi, hora noctis 2 1/2 quae sequitur diem qui fuit 2um Iunii 1547

Franciscus Maurolycus magno cum labore, vigiliisque correctum scribebat.

Inizio della pagina