37a Si coni sectionem, vel circuli periferiam, vel contrapositas duae lineae tangentes coincidant: et a coincidentia1 in lineam tactus ipsarum iungentem ducatur quaedam secans periferiam ad duo puncta; erit, ut tota ad extra receptam, sic factae portiones a iungente tactus.
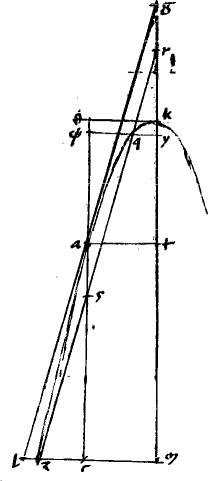
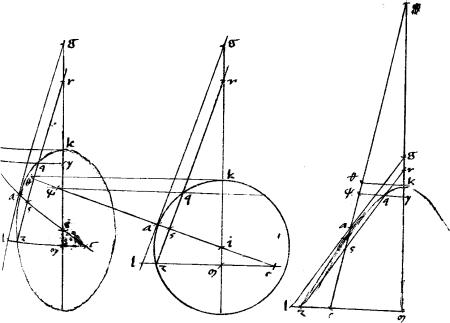
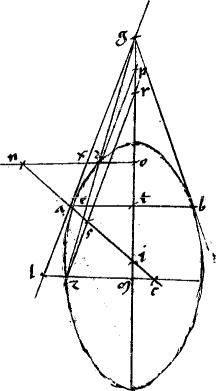
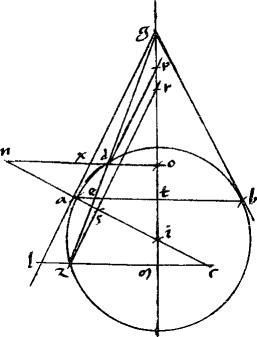
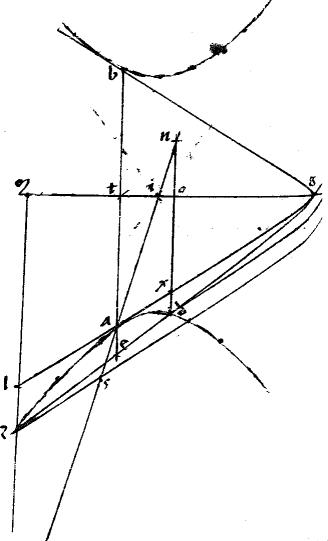
1 Sit coni sectio ab. // Tangentes agb. // Coniungens tactus ab. // Linea gdez secans periferiam sectionis apud d z puncta: ipsamque ab apud e. // Dico iam quod est, sicut zg 
gd sic ze ed. // Ducantur enim diametri sectionis gprotm nac in parabola quidem aequidistantes; in hyperbola, vero ellipsi, circulo, contrapositisque ad centrum i concurrentes. 2 // Item zr dp aequidistantes ipsi lag. // Nec non lzcm nxdo aequidistantes ipsi aetb tactus iungenti. // Eritque propter similitudinem triangulorum ut zg gd sic lz xd et sic zm do et sic lm xo. // Igitur ut 
lm xo sic zm do et propter similitudinem et proportionem figurarum sic 
lmg xog et sic 2 zrm dpo totum scilicet ad totum sicut ablatum ad ablatum. 3 // Quare, per 19am quinti Euclidis sic 
lgrz xgpd reliquum videlicet ad reliquum. // Aequale autem lgrz lo alc in parabola, quidem hyperbola, circulo et ellipsi, ut ostendit scholium adiectum: in contrapositis autem per 11am huius. // Item aequale xgpd lo anx in parabola videlicet, hyperbola, ellipsi, circuloque, per 2am huius: in contrapositis vero, per corollarium 11ae huius. 4 // Igitur, ut lm xo sic alc anx. // Verum propter similitudinem triangulorum ut lm xo sic zg gd. // Et propter proportionem figurarum, ut alc anx sic la ax et sic ze ed. // Itaque, ut zg gd sic ze ed. // Et, quoniam proportionalium quadratorum proportionalia sunt latera; ideo iam, et ut zg gd sic ze ed. 5 // Quod proponebatur demonstrandum. [A:86v]
4
]]5
]]6
7
8
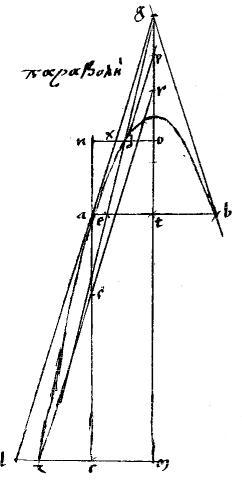
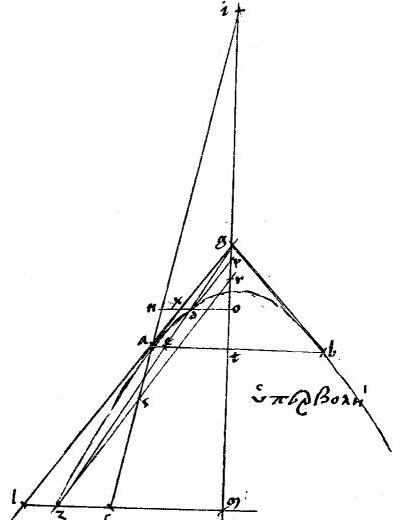
[A:87r] [S:116] Scholium
6 Superest nunc,ad complementum demonstrationis huius 37ae ostendere quod aequale est alc ipsi lgrz.
tangentem apud k et occurrentem ipsi ca diametro apud . 7 // Secet autem zr periferiam apud q et ipsi k aequidistantem duco q y. // Ipsamque zq secet ac diameter apud s. // Secabit autem bifariam in parabola quidem per 46am primi Conicorum, in caeteris, per 47am eiusdem. // Quo fit, ut s c z sq iam similia sunt et invicem aequilatera, et aequalia. // 8 Triangulum sq aequale est sagr in parabola quidem, per 42am primi Conicorum: in ceteris autem, per demonstrata in 47a eiusdem11 // Igitur et scz aequale erit12 eidem sagr. // Commune apponatur lasz. // Et conflabitur totum alc aequale iam toti lgrz. 9 // Quod quidem restabat demonstrandum. // Quod si varia punctorum et linearum positio casum variaret: adhuc accomodanda esset casui lineatio: lectorisque solertia adhibenda: incredibile enim memoratu est, quam variae descriptiones cuivis apolloniano theoremati sint necessariae.
