F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  i  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Emendatio et restitutio Apollonii Pergaei conicorum elementorum Liber tertius Propositio 20
<- App. -> <- = ->

1 20a Si contrapositas duae lineae tangentes coincidant: et per concursum ducatur quaedam linea penes tactus coniungentem coincidens utrique sectionum: ducatur autem alia quaedam linea penes ipsas secans sectiones et tangentes; erit, ut contentum1 sub lineis, quae a concursu sectionibus coincidunt, ad quadratum, quod fit a tangente, sic contentum sub iis, quae inter sectiones et tangentem ad quadratum quod fit a recepta de tangente ad tactum.

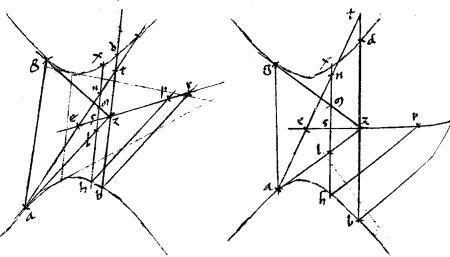figura 1
2 Sint contrapositae ab, gd. // Centrum e. // Tangentes az, gz. // [A:74v] Et coniugatur ag. // Et ez, ae et producantur. // Et ducatur per z penes2 ag linea bzdt3 occurens ipsi ae productae apud t4. // Et a relicto puncto h in sectione ducatur penes ag linea hlsmnx secans scilicet ipsam az apud l ipsam ez apud s ipsam gz apud m ipsam ed apud n sectionemque gd apud x. // 3 Dico iam quod est, ut quadrato5 bzd ad quadrato az sic rettangolo hlx ad quadrato al. // Ducantur enim penes az tangentem ipsae hp, br ad ipsam ez productam. // Et quoniam per 39am et 38am praemissi, ipsa eszpr coniugata diameter est diametro per e ductae penes ipsam ag ideo ipsae bd, hx applicatae sunt ad ipsam er diametrum. // Et perinde aequales sunt bz, zd item aequales hs, sx. // Quare, per 5am 2i Euclidis rettangolo hlx cum quadrato ls aequale est quadrato hs. 4 // Sed, propter figurarum similitudinem, sicut quadrato hs ad triangolo hsp totum scilicet ad totum; sic quadrato ls ad triangolo lsz ablatum ad ablatum. // Igitur, per 19am quinti Euclidis rettangolo hlx ad trapezio hlzp reliquum videlicet ad reliquum, sicut quadrato hs ad triangolo hsp totum ad totum: et, propter figurarum similitudinem, sicut quadrato bz ad triangolo bzr. // Verum, quoniam aequales bz zd aequale est6 quadrato bz rettangolo bzd. 5 // Item aequale est triangolo bzr triangololo azt7 per primam additarum praecedentium. // Adhuc aequum est trapezio hlzp triangololo aln per corollarium secundae huius. // Ergo, sicut quadrato8 bzd ad triangolo  azt9 sic est rettangolo hlx ad triangolo aln. // Ut autem triangolo azt10 ad quadrato az sic triangolo anl ad quadrato al. // Itaque ex aequali, sicut quadrato11 bzd ad quadrato az sic rettangolo hlx ad quadrato al. // Quod fuit demonstrandum.

Scholium

6 Si autem contingerit lineam hx transire per centrum e tunc triangolo anl sisteretur ad centrum: et tunc arguendam aequilitatem triangolo anl et trapezio hlzp uteremur praemissa immediate addita, in qua ostensum est tale trigonum ad centrum tali quadrilatero aequale esse.

Inizio della pagina
 ->