|
[A:55r] 48a Demonstratis utique his deinceps demonstrandum est, quod earumdem sectionum alii axes non sunt.
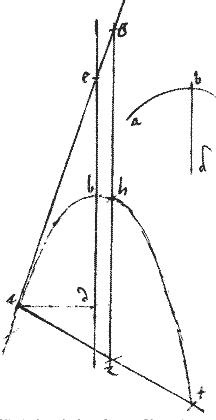 Si enim possibile est, sit alter axis ch ductaque, ut prius, katheto at erit per eadem at aequalis tl quare et ac aequalis cl. // Quod est absurdum.
Si enim possibile est, sit alter axis ch ductaque, ut prius, katheto at erit per eadem at aequalis tl quare et ac aequalis cl. // Quod est absurdum.
// Quod autem aeg1 circulus ad aliud punctum inter abg non coincidit sectioni, in hyperbole manifestum. // In ellipsi vero ketheti deducantur gr ls si possibile sit, ut et apud l punctum circulus sectioni coincidat: eruntque   cg cl aequalia. cg cl aequalia.
|
|
// Cumque per penultimam primi Euclidis  cg cg |
|
[S:74] aequale2. |
|
|
|
|
Et  cl cl |
|
aequale sit. |
|
|
Sit  3 x excessus, quo 3 x excessus, quo  rc superat4 rc superat4  cs eodemque et cs eodemque et  ls superabit ls superabit  gr. gr.
|
|
|
// Per 5am autem 2i Euclidis |
|
|
|
|
|
aequalia  mc cui aequalia5 mc cui aequalia5 |
|
. |
|
|
Igitur
 msn superat msn superat  mrn dicto excessu mrn dicto excessu  6 x. 6 x.
|
|
|
Quare |
|
aequalia  to ls to ls |
|
|
|
|
|
itemque |
|
aequalia  msn. msn. |
|
|
// Sed per 21am praecedentis libelli et permutatam proportionem, sicut  ls ls   gr sic gr sic  msn msn   mrn. mrn.
|
|
|
// Hoc est sicut |
|
simul   gr sic iam gr sic iam |
|
|
|
|
|
|
simul   mrn. mrn. |
|
|
// Et disiunctim sicut
 x x   gr sic gr sic  x x   mrn. // Quare per 9am 5i Euclidis mrn. // Quare per 9am 5i Euclidis  gr aequale est gr aequale est  mrn. // mrn. // |
|
Positoque communi  x erunt iam x erunt iam |
|
|
|
|
|
|
simul aequalia |
|
simul sumptis. |
|
|
Hoc est  ls aequale ls aequale  msn. msn.
// Itaque per lemma 5ae praemissi libri propositum, erit iam ipsa lg circuli periferia: quod est absurdum. Supponitur enim ellipsis. Non igitur circulus ellipsis supra axem mn alibi quam in punctis a g coincidit. // Quod erat demonstrandum.
Cum itaque, neque hyperbole, neque ellipsis alium, quam cd axim habeat: [A:55v] iam manifestum est, quod neque alium, quam mcn coniugatum axim habebit cum ipsi coniugati axes sint ad rectos.
|

![]()
![]() cg cl aequalia.
cg cl aequalia. ![]() 3 x excessus, quo
3 x excessus, quo ![]() rc superat4
rc superat4 ![]() cs eodemque et
cs eodemque et ![]() ls superabit
ls superabit ![]() gr.
gr. ![]() msn superat
msn superat ![]() mrn dicto excessu
mrn dicto excessu ![]() 6 x.
6 x. ![]() ls
ls ![]()
![]() gr sic
gr sic ![]() msn
msn ![]()
![]() mrn.
mrn. ![]() x
x ![]()
![]() gr sic
gr sic ![]() x
x ![]()
![]() mrn. // Quare per 9am 5i Euclidis
mrn. // Quare per 9am 5i Euclidis ![]() gr aequale est
gr aequale est ![]() mrn. //
mrn. //